深度学习笔记
参考文档:https://github.com/Elvin-Ma/deep_learning_theory
从感知机到神经网络
相关概念
人工智能是什么
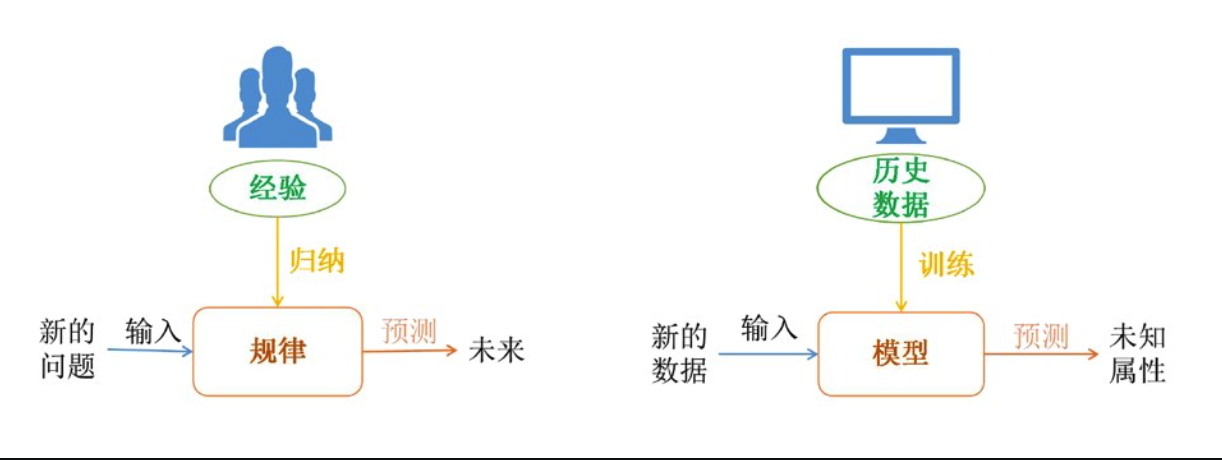
深度学习与人工智能的关系
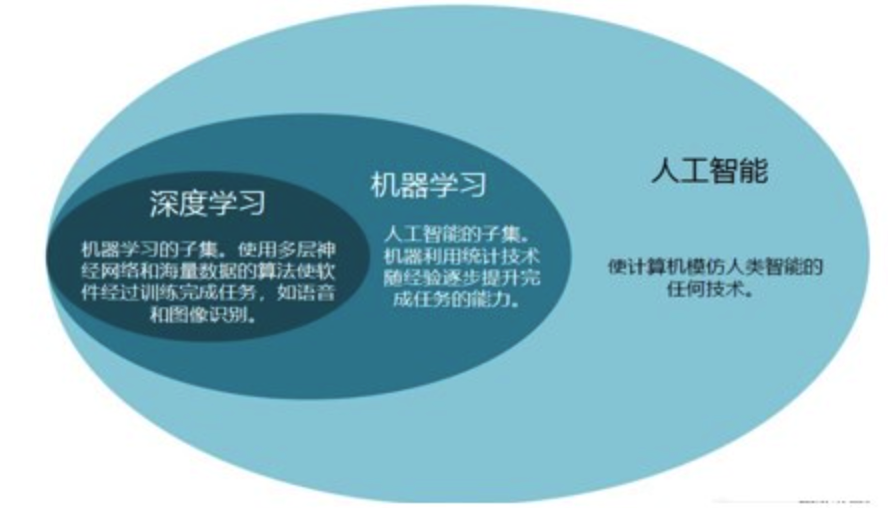
深度学习的概念
深度学习(deep learning)是机器学习的分支,是一种以人工神经网络为架构,对资料进行表征学习的算法。
在机器学习中,特征学习(feature learning)或表征学习(representation learning)[1]是学习一个特征的技术的集合:将原始数据转换成为能够被机器学习来有效开发的一种形式。它避免了手动提取特征的麻烦,允许计算机学习使用特征的同时,也学习如何提取特征:学习如何学习。
深度学习旨在通过构建和训练多层神经网络来实现人工智能任务。它模拟了人脑神经元之间的相互连接和信息传递方式,通过学习大量数据来提取特征和模式,并用于分类、识别、预测和决策等任务。
什么是人工神经网络
人工神经网络(artificial neural network,ANNs)简称神经网络(neural network,NNs)或类神经网络,在机器学习和认知科学领域,是一种模仿生物神经网络(动物的中枢神经系统,特别是大脑)的结构和功能的数学模型或计算模型,用于对函数进行估计或近似。
神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构,是一种自适应系统,通俗地讲就是具备学习功能。
现代神经网络是一种非线性统计性数据建模工具,神经网络通常是通过一个基于数学统计学类型的学习方法(learning method)得以优化,所以也是数学统计学方法的一种实际应用,通过统计学的标准数学方法我们能够得到大量的可以用函数来表达的局部结构空间,另一方面在人工智能学的人工感知领域,我们通过数学统计学的应用可以来做人工感知方面的决定问题(也就是说通过统计学的方法,人工神经网络能够类似人一样具有简单的决定能力和简单的判断能力),这种方法比起正式的逻辑学推理演算更具有优势。
前馈神经网络的概念
深度前馈网络(deep feedforward network), 也叫作前馈神经网络(feedforward neural network)或者多层感知机(multilayer perceptron, MLP), 是典型的深度学习模型。
神经元模型
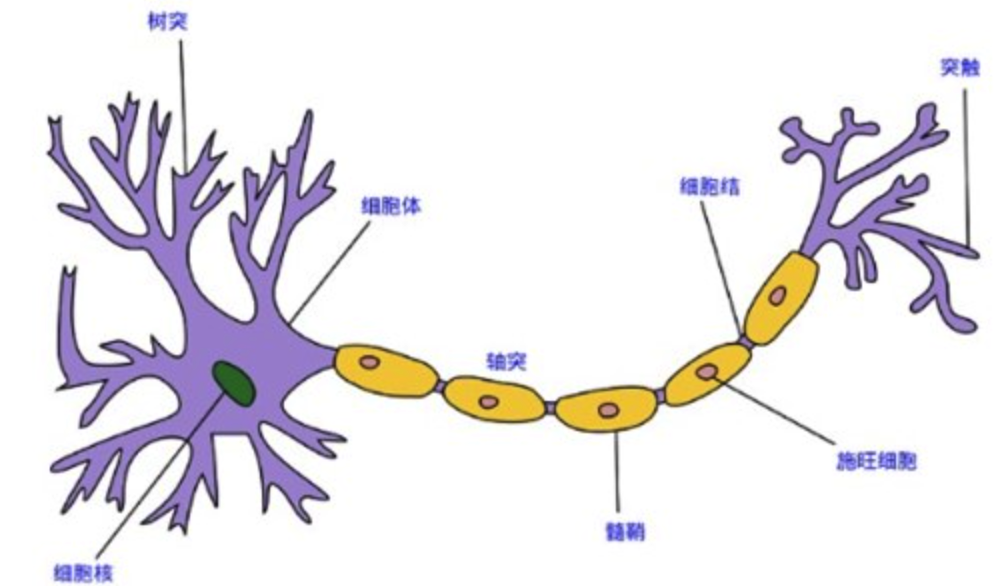
1943 年,[McCulloch and Pitts, 1943] 将神经元抽象为数学概念上的的简单模型,这就是一直沿用至今的 M-P 神经元模型:
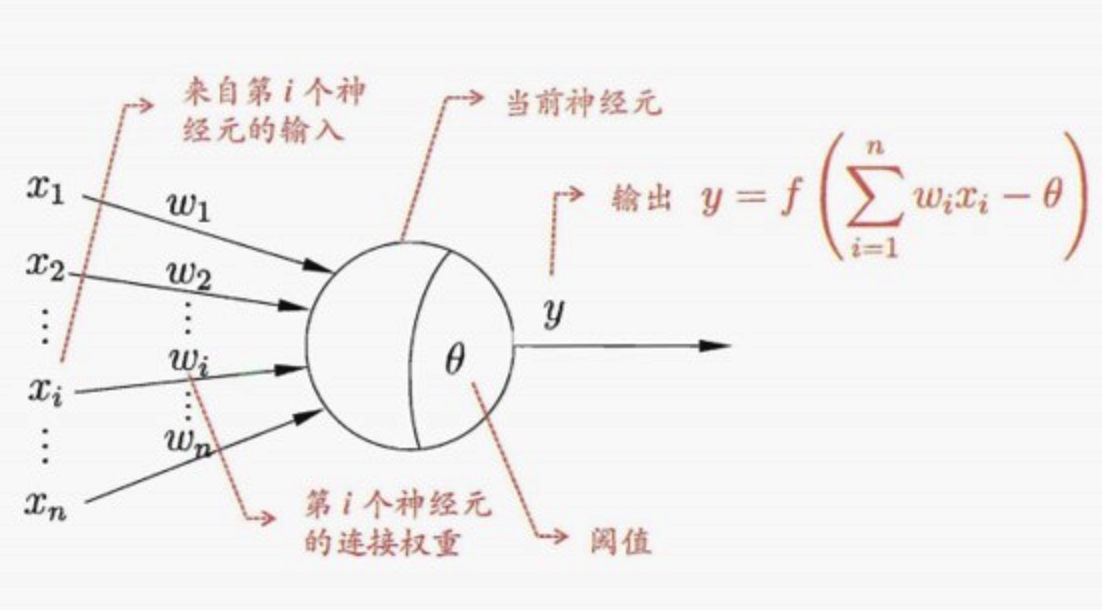
在这个模型中, 神经元接收到来自 n 个其他神经元传递过来的输入信号, 这些输入信号通过带权重的连接(onnection)进行传递,神经元接收到的总输入值(sum)将与神经元的阀值进行比较,然后通过激活函数(activation function) 处理以产生神经元的输出。
经典激活函数
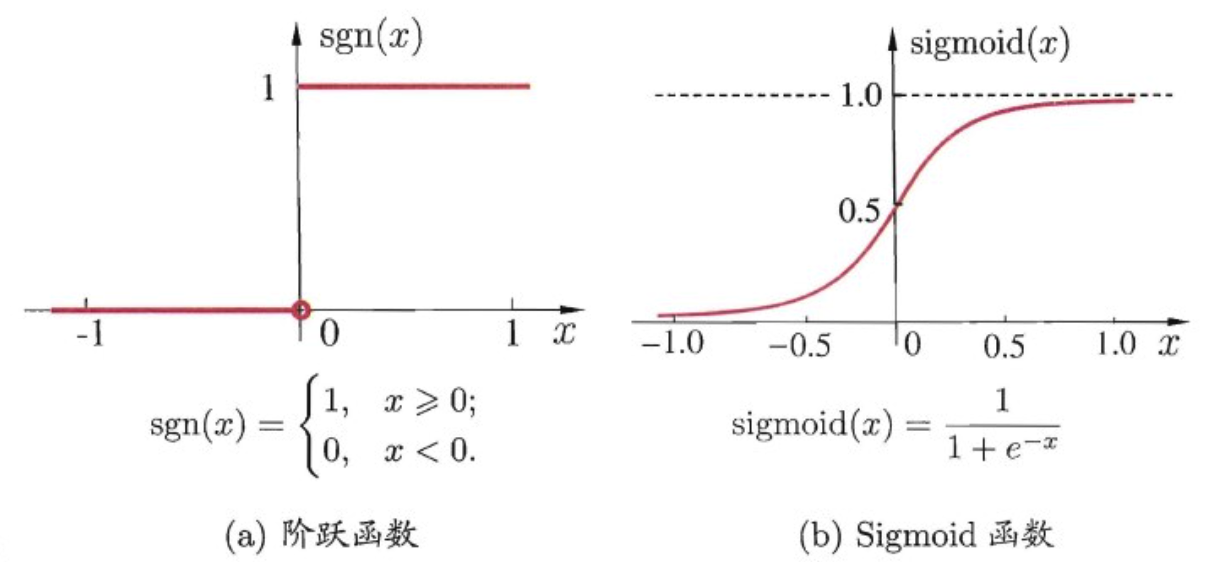
最初的激活函数是下图左所示的阶跃函数,它将输入值映射为输出值 0 或 1, 显然 "1" 对应于神经元兴奋, "0" 对应于神经元抑制. 然而,阶跃函数具有不连续、不光滑等不太好的性质,因此实际常用Sigmoid函数作为激活函数(注释:目前已经有很多更好的激活函数)。 典型的Sigmoid 函数如图下图右所示, 它把可能在较大范围内变化的输入值挤压到(0,1) 输出值范围内,因此有时也称为"挤压函数(squashing function)"。
从神经元到感知机
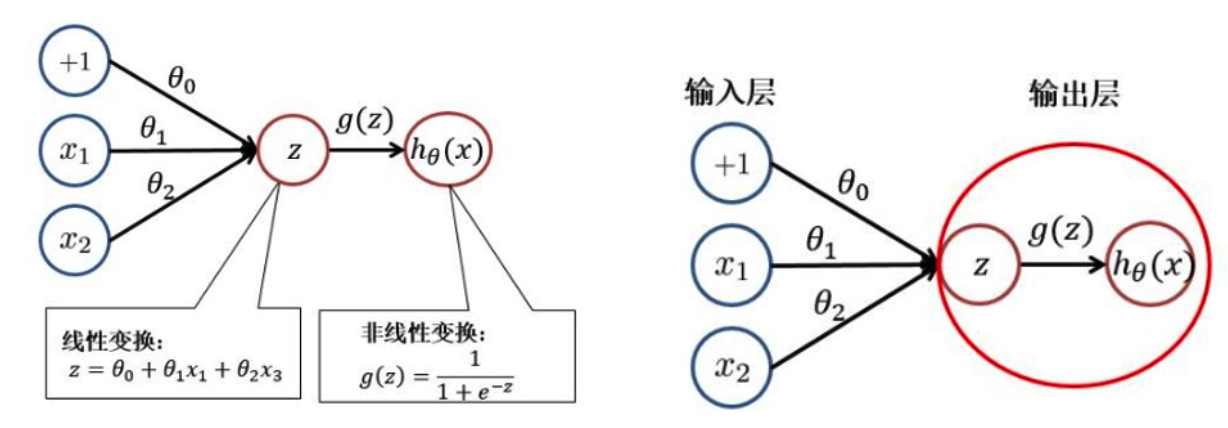
感知机(perceptron)是由两层神经元组成的结构,输入层用于接受外界输入信号,输出层(也被称为是感知机的功能层)就是M-P神经元,亦称“阈值逻辑单元”(threshold logic unit)。
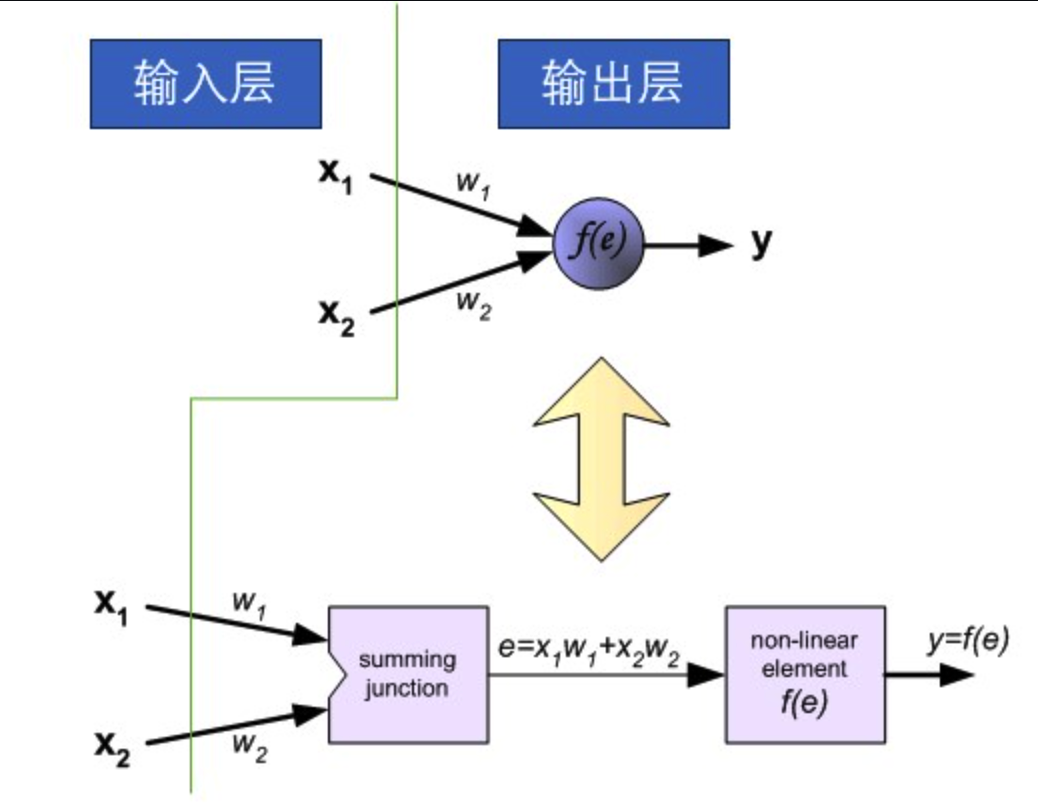
从感知机到深度神经网络
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制, 使其能处理更普遍的函数关系类型。 要做到这一点,最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层,直到生成最后的输出。 我们可以把前L−1层看作表示,把最后一层看作线性预测器。 这种架构通常称为多层感知机(multilayer perceptron),通常缩写为MLP。
更一般的,常见的神经网络是形如下图所示的层级结构,每层神经元与下层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接. 这样的神经网络结构通常称为多层前馈神经网络(multi-layer feedforward neural network)
习惯上,我们通常将 Layer 大于两层的 MLP 或 MultiLayer feedforward neural network 简称为深度神经网络,其典型结构如下图所示:
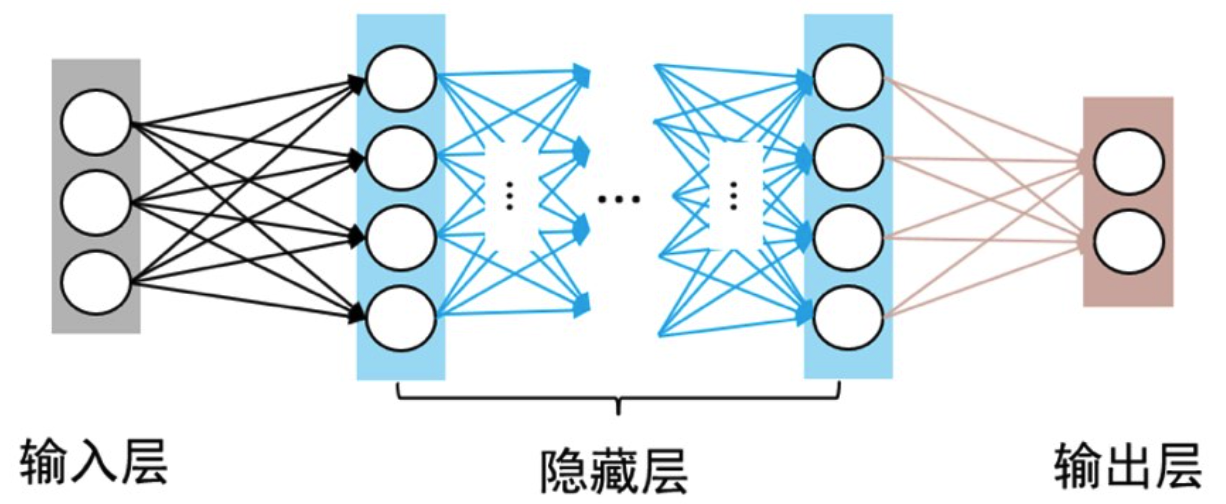
为何要用深度神经网络?
理论和实践都反复证明,随着隐层的增加,模型的表征能力也会增加,可以解决的问题也更加广泛
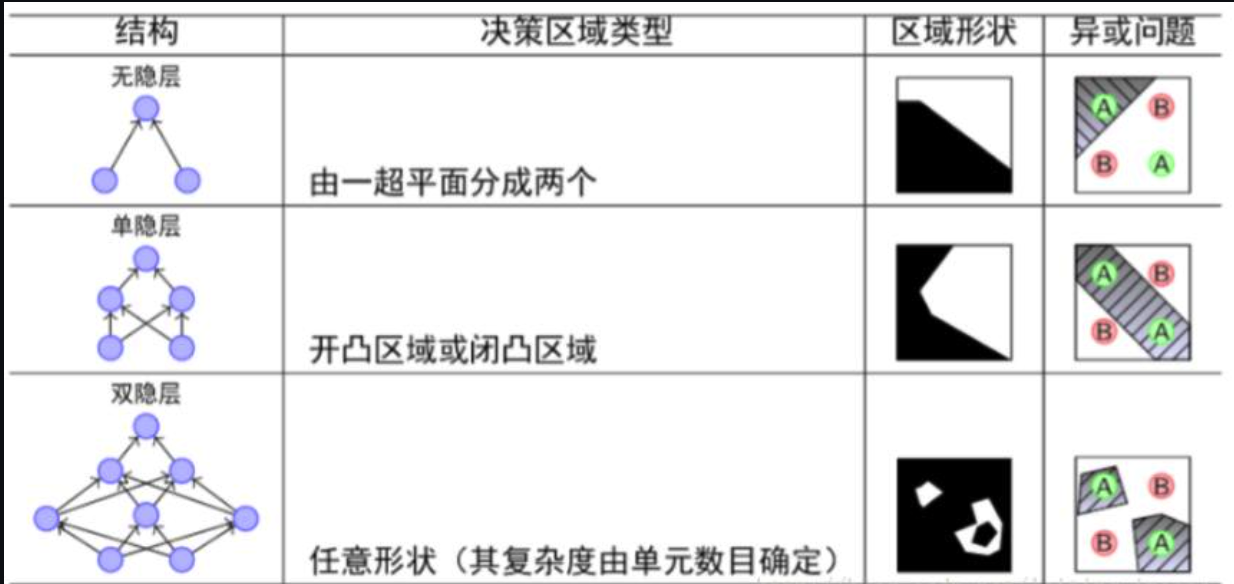
随着隐层层数的增多,凸域将可以形成任意的形状,因此可以解决任何复杂的分类问题。实际上,Kolmogorov理论指出:双隐层感知器就足以解决任何复杂的分类问题。于是我们可以得出这样的结论:神经网络通过将线性分类器进行组合叠加,能够较好地进行非线性分类。
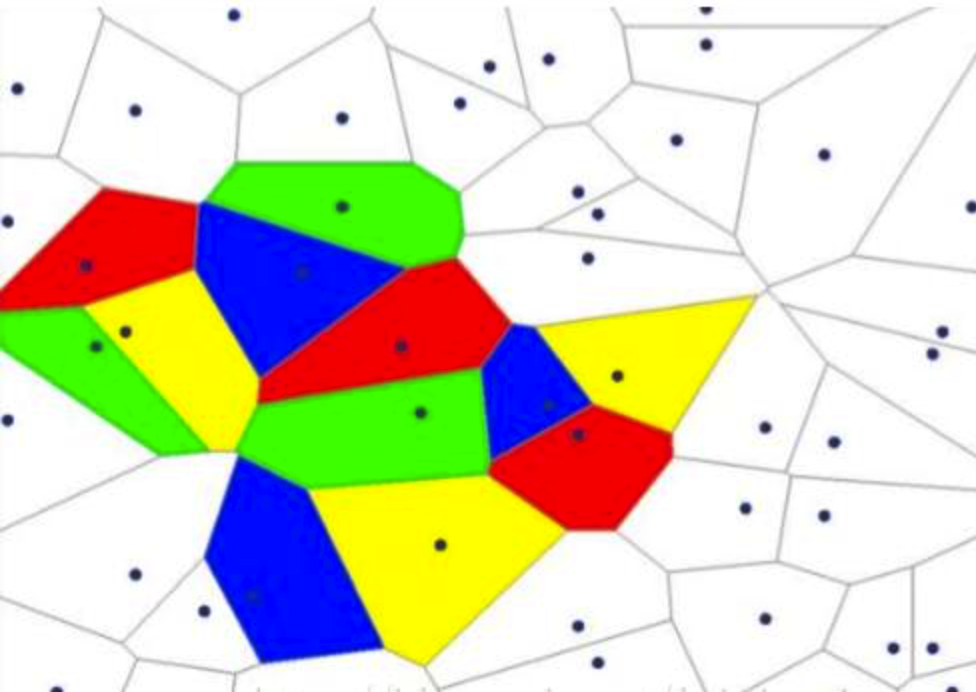
深度神经网络解决问题案例
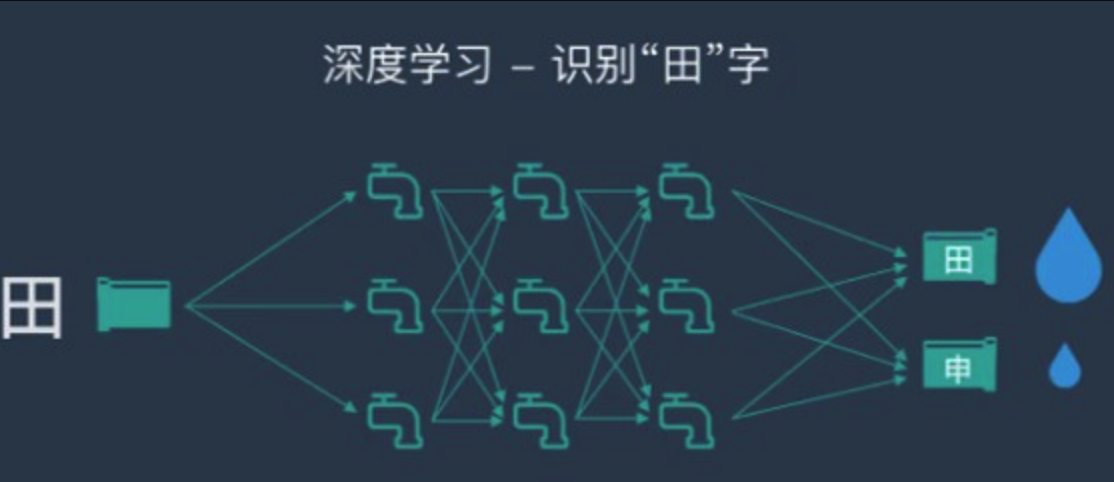
假设深度学习要处理的信息是“水流”,而处理数据的深度学习网络是一个由管道和阀门组成的巨大水管网络。网络的入口是若干管道开口,网络的出口也是若干管道开口。这个水管网络有许多层,每一层由许多个可以控制水流流向与流量的调节阀。根据不同任务的需要,水管网络的层数、每层的调节阀数量可以有不同的变化组合。对复杂任务来说,调节阀的总数可以成千上万甚至更多。水管网络中,每一层的每个调节阀都通过水管与下一层的所有调节阀连接起来,组成一个从前到后,逐层完全连通的水流系统。
深度神经网络识别汉字
前馈神经网络计算流程
第一层计算

第二层计算
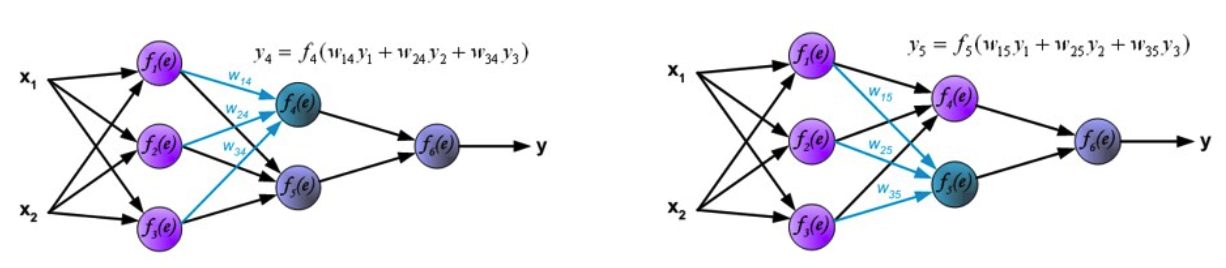
第三层计算
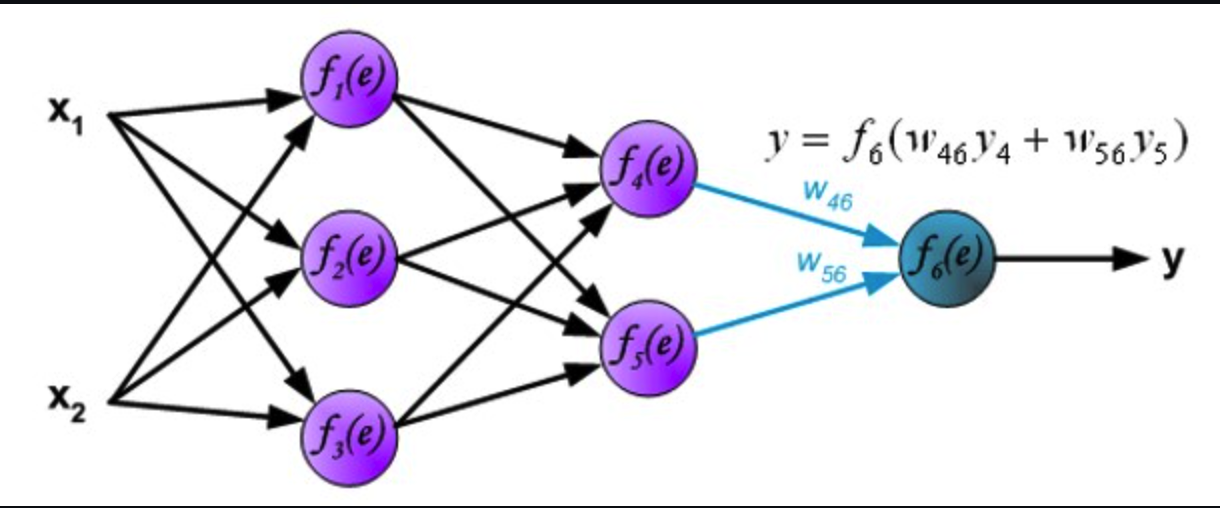
深度学习与传统机器学习
相同点
在概念、数据准备和预处理方面,两者是很相似的,他们都可能对数据进行一些操作:
- 数据清洗
- 数据标签
- 归一化
- 去噪
- 降维
不同点
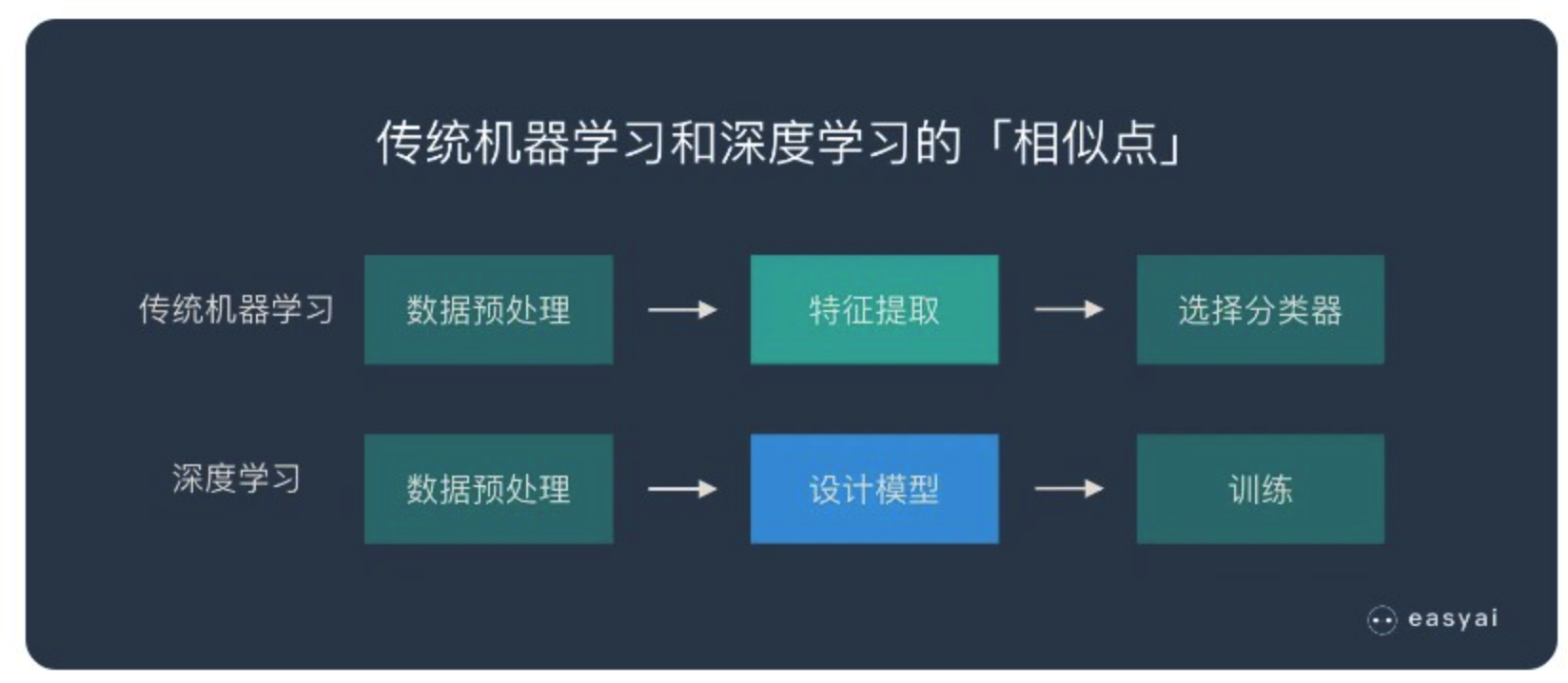
- 传统机器学习的特征提取主要依赖人工,针对特定简单任务的时候人工提取特征会简单有效,但是并不能通用。
- 深度学习的特征提取并不依靠人工,而是机器自动提取的。这也是为什么大家都说深度学习的可解释性很差,因为有时候深度学习虽然能有好的表现,但是我们并不知道他的原理是什么。
深度学习的典型算法
- CNN 能够将大数据量的图片有效的降维成小数据量(并不影响结果),能够保留图片的特征,类似人类的视觉原理;
- RNN 是一种能有效的处理序列数据的算法。比如:文章内容、语音音频、股票价格走势…;
- GAN 是一种深度学习架构。 该架构训练两个神经网络相互竞争,从而从给定的训练数据集生成更真实的新数据;
- 强化学习(Reinforcement learning,简称RL) 强调如何基于环境而行动,以取得最大化的预期利益,强化学习不需要带标签的输入输出对,而是通过自己不停的尝试来学会某些技能。
2017 年 出现了 Transfomer 模型,取得了重大成功,深度学习的众多项任务都开始应用 Transfomer 算法。
反向传播
神经网络训练流程概述
当我们使用前馈神经网络(feedforward neural network)接收输入
在训练过程中,前向传播可以持续向前直到它产生一个 标量 的损失函数
反向传播(back propagation)算法经常简称为backprop,允许来自代价函数的信息通过网络向后流动,以便计算梯度。
反向传播不会更新参数,但是能求得每个参数的梯度值,然后根据梯度值来更新参数
梯度下降算法简述
多元函数
函数
梯度下降算法的基本过程:
- 初始化(定义)学习率
和初始参数 - while
小批量样本 对应的 Label 计算平均梯度 表示模型的参数 的梯度,通常是一个向量,表示损失函数关于 的偏导数 表示训练样本的总数 表示损失函数,是模型预测结果与实际标签之间的误差,这里 是模型在输入样本 下预测的结果,而 是样本 的实际标签
更新参数
Pytorch 安装
PyTorch 是一个 Python 包,它提供了两个高级功能:
- 利用强大的 GPU 加速进行张量计算(例如 NumPy)。
- 基于磁带式自动微分系统的深度神经网络

使用 pip 安装
常见的深度学习算子
线性变换层
Linear/Gemm
对输入数据应用仿射线性变换:

import torch
import torch.nn as nn
m = nn.Linear(20, 30)
input = torch.randn(128, 20)
output = m(input)
print(output.size())
torch.Size([128, 30])
注意,Linear 在设置参数的时候,是带转置的
linear = nn.Linear(20, 30)
linear.weight.shape
torch.Size([30, 20])
表示
matmul
matmul 不在 torch.nn 里
对于 matmul 来说,第一个输入和第二个输入是等价的,但是对于线性层,一个代表输入,一个代表权重
pytorch中有三个相似的矩阵操作
- matmul是通用的矩阵乘法函数,适用于不同维度的输入。
- bmm是用于批量矩阵乘法的函数,要求输入为3维张量。
- mm是用于两个二维矩阵乘法的函数,要求输入为2维张量。
import torch
tensor1 = torch.randn(10, 3, 4)
tensor2 = torch.randn(10, 4, 5)
torch.matmul(tensor1, tensor2).size()
torch.Size([10, 3, 5])
Normalization
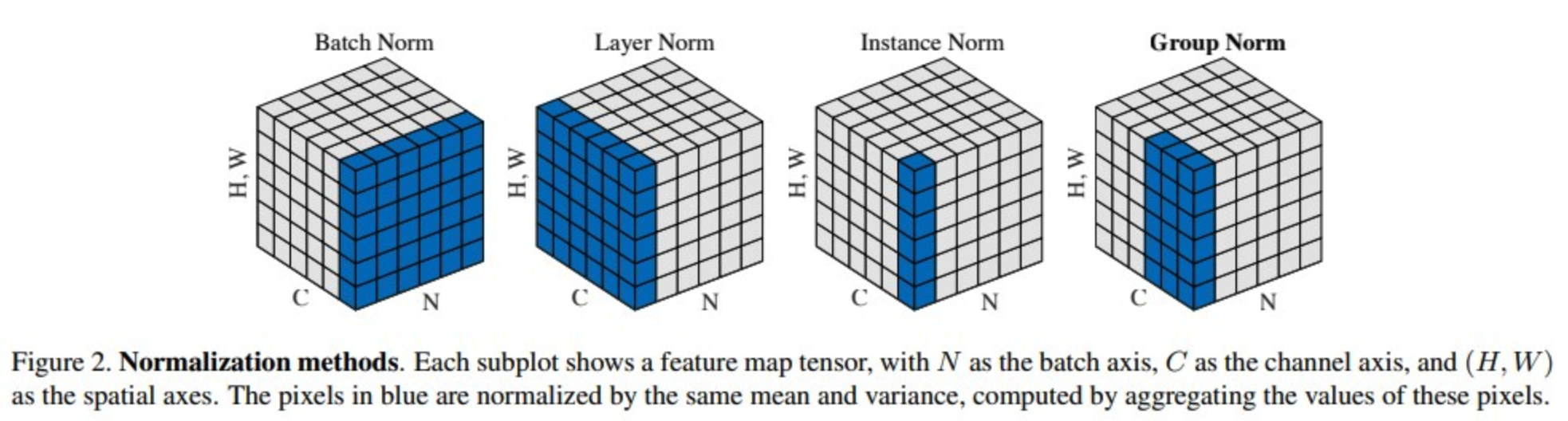
BatchNorm2d
BatchNorm2d 是对 4D 特征图做归一化(normalization) 的层,输入形状通常是
- N 是batch size
- C 是通道数
- H, W:特征图的高和宽
它会对 每个通道 C 分别做标准化,使得激活值分布更稳定,加快训练速度,同时有正则化效果。
对于每一个通道 C:
- 先求 batch 的均值和方差
- 然后对该通道归一化
- 再进行线性变换(可学习参数)
和 都是可以学习的参数
其最常用的做法就是接在卷积层的后面
import torch
import torch.nn as nn
bn = nn.BatchNorm2d(num_features=64)
x = torch.randn(8, 64, 32, 32) # N,C,H,W
y = bn(x)
print(y.shape)
torch.Size([8, 64, 32, 32])
num_features=64表示对 64 个通道都进行归一化操作
BatchNorm 有两个阶段,训练模式和推演模式
训练模式
使用 当前 batch 的均值和方差 running_mean running_var 这些是为了推理用的。
推理模式
使用 running_mean 和 running_var,而不使用 batch 的统计量。
因为推理 batch 可能是 1,统计意义不稳定。
来看一下 BatchNorm2d 的参数解释
nn.BatchNorm2d(
num_features,
eps=1e-5,
momentum=0.1,
affine=True,
track_running_stats=True
)
- num_features: 通道数C
- eps:防止除 0
- momentum:更新 running 均值和方差的速度
- affine=True → 允许 γ 和 β(可训练)
- track_running_stats=True → 保存 running 均值和方差
LayerNorm
LayerNorm(层归一化) 是一种归一化方法,它对 同一个样本的所有特征维度 进行归一化。
它最早用于 RNN、Transformer 等序列模型中,因为它不依赖 batch 的统计值。
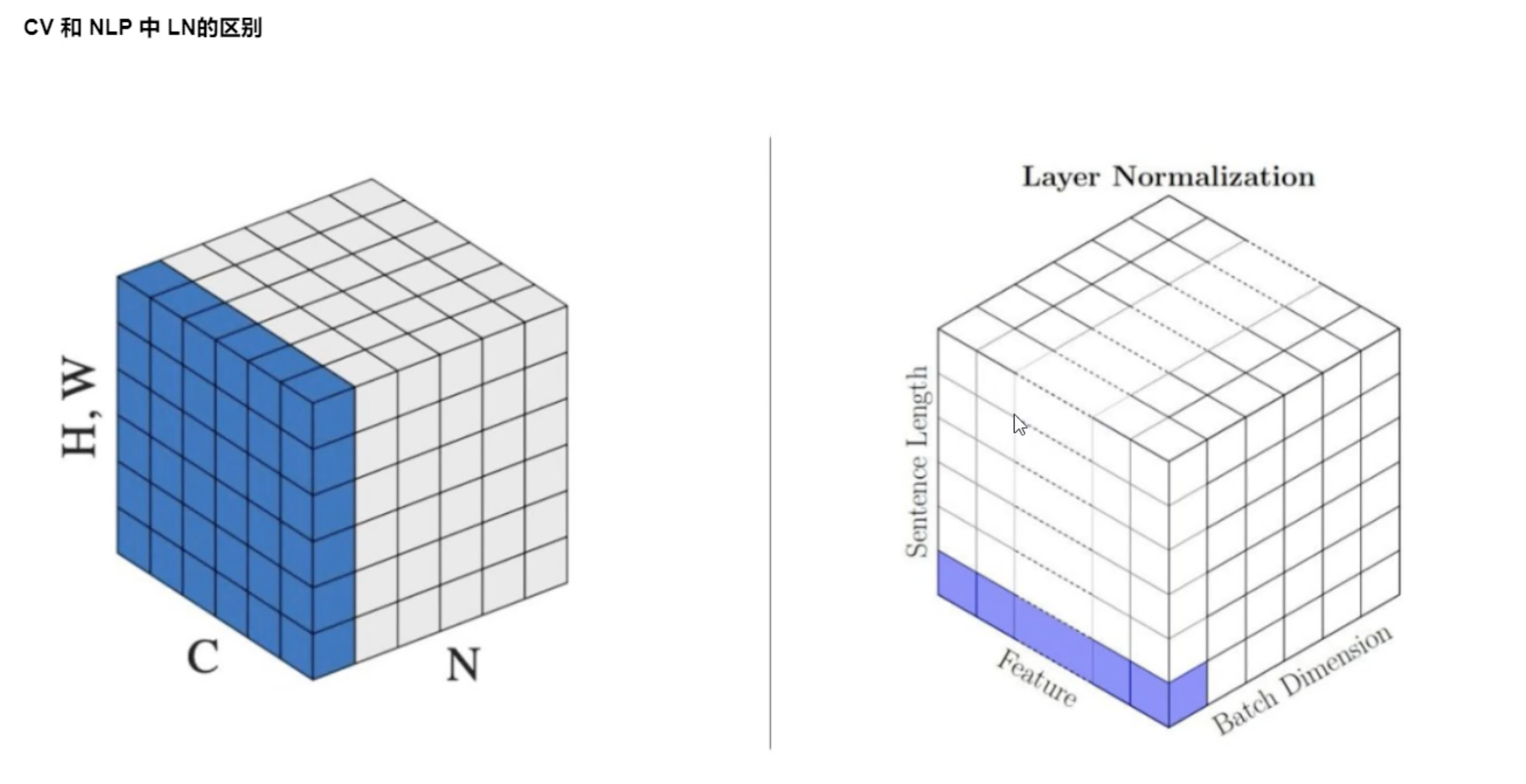
LayerNorm 和 BatchNorm 的本质区别
| 方法 | 归一化范围(非常重要) | 依赖batch大小? | 最常用场景 |
|---|---|---|---|
| BatchNorm | 对同一个通道的所有样本进行归一化 | ✓ 依赖batch | CNN |
| LayerNorm | 对同一个样本的所有特征归一化 | × 不依赖batch | Transformer/NLP/RNN |
- BatchNorm:跨样本做归一化
- LayerNorm:对每个样本单独做归一化
来看一下 LayerNorm 的过程
对于某个样本的特征
- 计算当前样本的均值
- 计算当前样本的方差
- 归一化
- 再进行缩放与偏移(可训练)
LayerNorm 在不同输入维度下如何工作?
PyTorch 中典型输入为:
(N, C, H, W)
LayerNorm 的归一化方式是:对后面的维度归一化(用户指定的 normalized_shape)
PyTorch 中使用 LayerNorm 的方式
示例 1:对一个 768 维向量归一化(如 Transformer)
import torch
import torch.nn as nn
ln = nn.LayerNorm(768) # 对最后一维做归一化
x = torch.randn(2, 10, 768) # batch=2, seq_len=10, hidden=768
y = ln(x)
print(y.shape) # torch.Size([2, 10, 768])
示例 2:在 CNN 中使用 LayerNorm(不常见)
ln = nn.LayerNorm([64, 32, 32]) # C,H,W
x = torch.randn(8, 64, 32, 32)
y = ln(x)
print(y.shape)
Instance Normalization
**Instance Normalization(实例归一化)**是一种在 CNN 中使用的归一化方法。
对每一个样本的每一个通道,单独做 H×W 维度的归一化。也就是说,即使 batch 中有多个样本,它也不会相互影响。
假设输入是 4D 张量:
InstanceNorm 会对每个样本、每个通道做如下归一化:
- 不跨 batch
- 不跨通道
- 只在 (H, W) 上计算 mean / var
对于每个样本的每个通道,把整张 feature map 归一化。
InstanceNorm 和 BatchNorm 的区别:
| 方法 | 归一化范围 | 是否依赖batch? | 典型场景 |
|---|---|---|---|
| BatchNorm | 跨batch、跨HxW | ✓ 依赖batch | 分类、检测CNN |
| InstanceNorm | 每样本、每通道、在HxW上归一化 | × 不依赖batch | 风格迁移、生成模型 |
| LayerNorm | 每样本所有特征 | × 不依赖batch | Transformer |
| GroupNorm | 每样本每组通道 | × 不依赖batch | 小batch CNN |
BatchNorm 用在 判别模型(分类)。
InstanceNorm 用在 生成模型(风格迁移、GAN)。
最常见用法:
import torch
import torch.nn as nn
norm = nn.InstanceNorm2d(64) # 64 个通道
x = torch.randn(8, 64, 32, 32)
y = norm(x)
print(y.shape)
默认情况 γ 和 β 是没有学习的(这个和 BatchNorm 不一样),但你可以开启:
nn.InstanceNorm2d(64, affine=True)
Group Normalization
Group Normalization(GN) 是一种替代 BatchNorm 的归一化方式,由 Facebook AI 在 2018 年提出。
它解决 BatchNorm 在 batch size 很小(如目标检测、分割、GAN 中常常 batch=1~4)时效果变差的问题。
核心 idea:把通道分组,而不是依赖 batch。
对于一个卷积网络的某层其形状是
如果 C=32,groups=4,则
- 每组包含 32/4 = 8 个通道
- GN 会对每一组的 (N, group_channels, H, W) 进行归一化
每一组分别统计均值和方差,然后做归一化
Pooling
Pooling(池化)是CNN 中常用的操作,通过在特定区域内对特征进行(reduce)来实现的。
作用
- 增大网络感受野
- 减小特征图尺寸,但保留重要的特征信息
- 抑制噪声,降低信息冗余
- 降低模型计算量,降低网络优化难度,防止网络过拟合
- 使模型对输入图像中的特征位置变化更加鲁棒
Max Pooling
最大池化在每个池化窗口中选择最大的特征值作为输出,提取特征图中响应最强烈的部分进入下一层
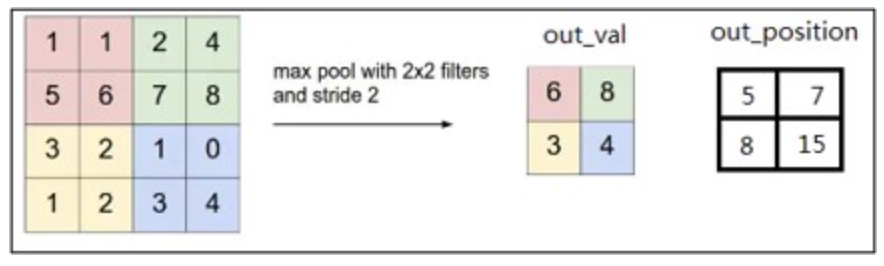
这种方式摒弃了网络中大量的冗余信息,使得网络更容易被优化。同时这种操作方式也常常丢失了一些特征图中的细节信息,所以最大池化更多保留些图像的纹理信息。
AveragePooling
平均池化在每个池化窗口中选择特征值的平均值作为输出,这有助于保留整体特征信息,可以更多的保留图像的背景信息,但可能会丢失一些细节。
reshape、 view、 permute、transpose
reshape
reshape(重塑) 是深度学习中非常常见的一个张量操作,用来在不改变数据内容的前提下,改变张量的形状(shape)
例如你可以把一个 shape 为
reshape 只改变对数据的“看法”,不复制数据,也就是说,数据还在原地址上
我们可以使用
原 shape: (2, 3, 4)
目标: reshape(2, -1)
→ -1 = 3*4 = 12
→ 结果 shape = (2, 12)
view
view() 和 reshape() 都能改变张量的形状,但:view() 是更严格的 reshape:只能对“连续内存”的 Tensor 进行形状重塑。
- view = 不复制内存的 reshape
- reshape = 更通用,不一定连续时会复制内存
为什么要连续内存(contiguous)?
Tensor 在内存中是按一定顺序排布的。如果你通过:
transposepermutesqueeze/unsqueeze- 切片操作(如
x[:, :3])
这些操作改变了内存访问方式,使得 Tensor 不再是连续存储,这时你不能直接 view(),会报错,例如
x = torch.randn(2, 3)
y = x.transpose(0, 1)
y.view(6) # 会报错:RuntimeError: view size is not compatible with input tensor
如何解决非连续问题?
使用 .contiguous()
y = x.transpose(0, 1).contiguous().view(6)
contiguous() 会重新拷贝一次张量,使内存变成连续,从而允许 view()。
view() 不改变张量在内存中的内容,只改变:我应该如何解读这块内存
| 特性 | view | reshape |
|---|---|---|
| 是否要求内存连续 | 是 | 否 |
| 是否一定不copy内存 | 是 | 不一定(可能copy) |
| 遇到非连续内存 | 会报错 | 会自动处理(必要时copy) |
| 性能 | 更快 | 略慢 |
| 安全性/灵活性 | 限制多 | 更灵活 |
transpose
transpose:维度交换算子,它会将 Tensor 的 两个维度互换,相当于多维张量的“转置”
(N, C, H, W) → (N, H, C, W)
transpose 只交换两个维度,不会复制数据,只改变 stride(内存访问方式)。
基本使用方法
x.transpose(dim0, dim1)
import torch
x = torch.randn(2, 3, 4)
y = x.transpose(0, 1)
print(x.shape) # [2, 3, 4]
print(y.shape) # [3, 2, 4]
permute
permute() 是 PyTorch 中的:多维张量的任意维度重排(Reorder)算子。
- transpose 只能交换两个维度
- permute 可以任意排列所有维度
permute 的用法格式
x.permute(dim0, dim1, dim2, ...)
- 指定所有维度的新顺序
- 维度数必须和原张量一致