90.最小斯坦纳树

给出一个无向联通图 $G=(V,E)$，和一个包含 $k$ 个节点的点集 $S$，包含点集 $S$ 的联通子图就是斯坦纳树，那么最小的联通子图，也就是最小斯坦纳树。

这个问题是 NP- hard，我们只有近似多项式的解法

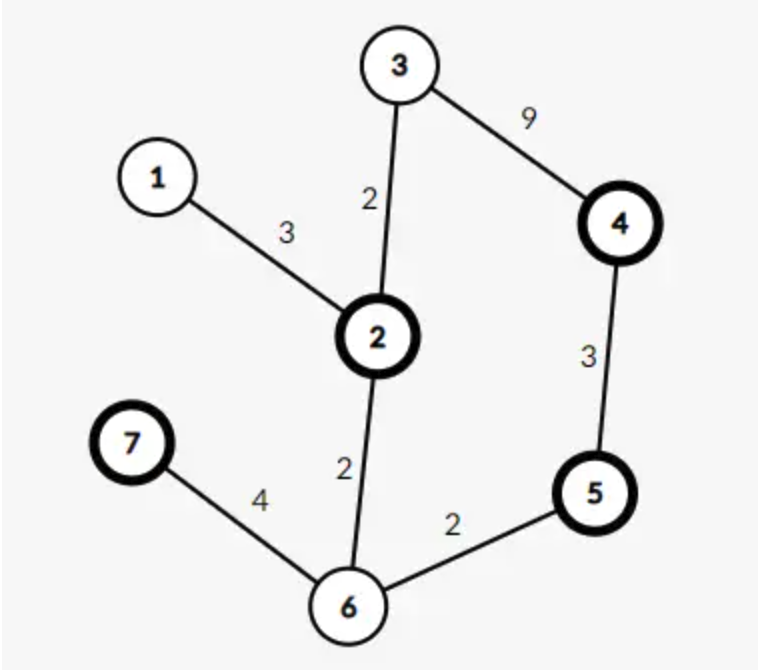
在这个图中，最小斯坦纳树的值为 11，整棵树长这样：

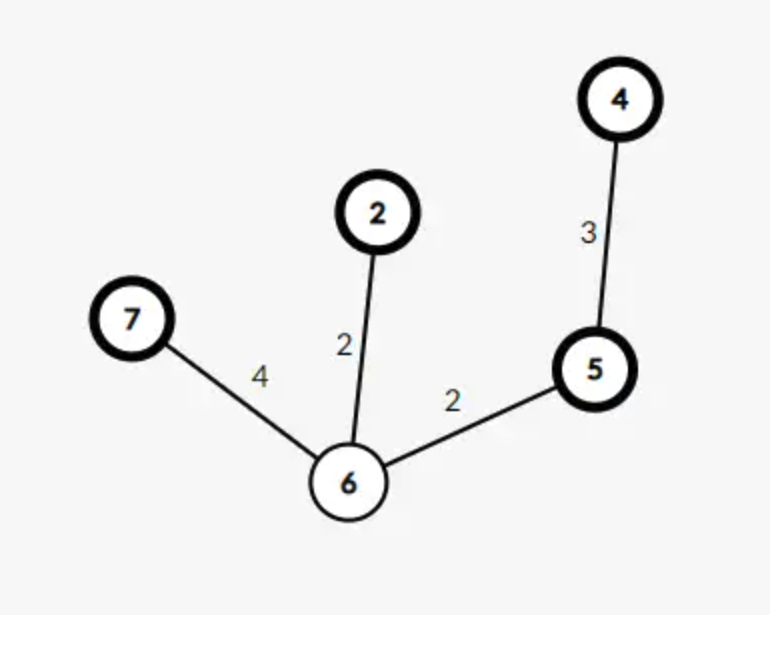
我们发现除了点集 $S$ 中的点，还包含了图上的点 $6$，所以我们应该思考如何合理利用剩下的 $n-k$ 个点

我们使用状压 DP 来解决这个问题，定义 $f(i,S)$ 表示以 $i$ 为根结点的一棵树，包含集合 $S$ 中所有点的最小权值和

那么有两种转移：

• 枚举 $S$ 的一个子集 $T$，$f(i,T)+f(i,S-T))\to f(i,S)$
• 枚举 $i$ 的所有边，$f(i,S)+w(j,i)\to f(j,S)$

第一个可以枚举子集来转移，时间复杂度是 $O(n{3}^k)$

第二个类似于三角形不等式，可以使用 SPFA 来解决，时间复杂度是 $O(nm{2}^k)$

代码实现

洛谷 P6192 【模板】最小斯坦纳树

#include <bits/stdc++.h>
using namespace std;
constexpr int INF = 0x3f3f3f3f;

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    int N, M, K; cin >> N >> M >> K;
    vector<vector<pair<int, int>>> g(N + 1);
    vector<vector<int>> dp(N + 1, vector<int>(1 << K, INF));
    vector<int> p(K + 1);
    for (int i = 1; i <= M; i++)  {
        int u, v, w; cin >> u >> v >> w;
        g[u].push_back({v, w}); g[v].push_back({u, w});
    }
    for (int i = 1; i <= K; i++) {
        cin >> p[i];
        dp[p[i]][1 << (i - 1)] = 0;
    }
    queue<int> q;
    vector<int> vis(N + 1, 0);
    for (int S = 0; S < (1 << K); S++) {
        for (int i = 1; i <= N; i++) {
            for (int S_ = S; S_; S_ = (S_ - 1) & S) {
                dp[i][S] = min(dp[i][S], dp[i][S_] + dp[i][S ^ S_]);
            }
            if (dp[i][S] < INF)
                q.push(i), vis[i] = 1;
        }
        while (!q.empty()) {
            int u = q.front(); q.pop(); vis[u] = 0;
            for (auto [v, w] : g[u]) {
                if (dp[v][S] > dp[u][S] + w) {
                    dp[v][S] = dp[u][S] + w;
                    if (!vis[v])
                        q.push(v), vis[v] = 1;
                }
            }
        }
    }
    cout << dp[p[1]][(1 << K) - 1] << '\n';
    return 0;
}