50.网络流

网络流

最大流问题

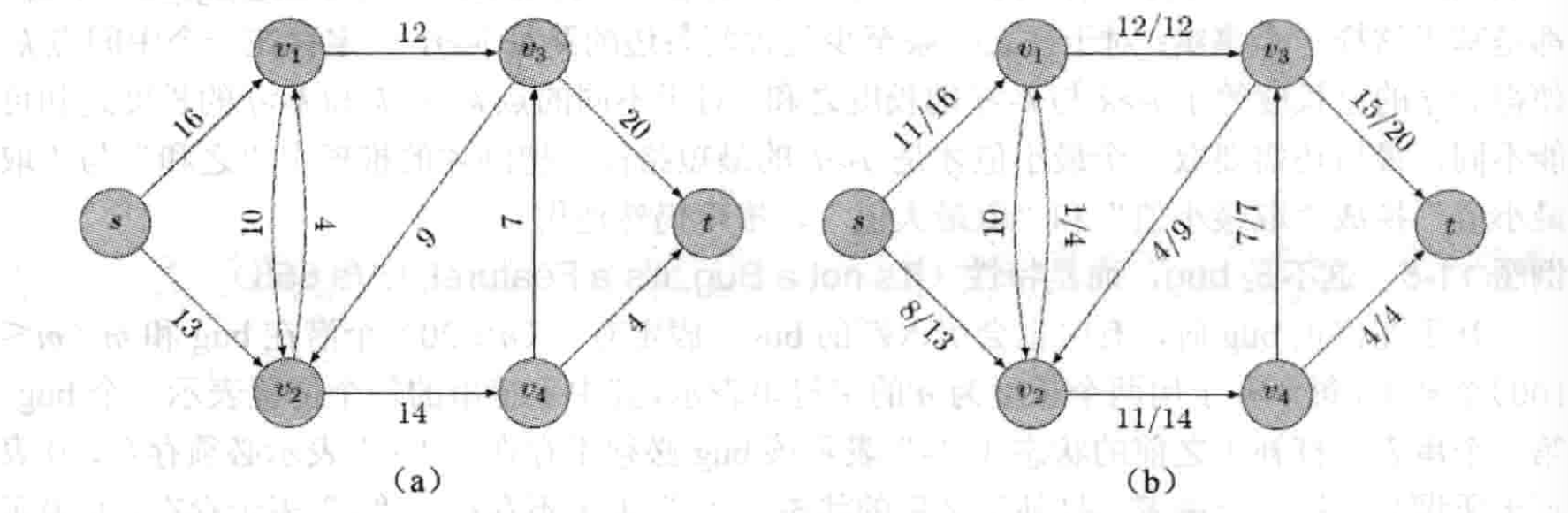
如图，我们需要把一些物品从节点 $s$ （称为源点），运送到节点 $t$ （称为汇点），可以从其他节点中转，图 a 中每条边上的数字表示每条边最多能运送几个物品

图 b 展示了一种可能的方案，每一条边的第一个数字表示实际运送的物品数目，称为流量记录 $f (u, v)$ ，第二个数字表示上限，称为容量 $c (u, v)$ ，对于不存在的边，我们记 $c (u, v) = 0$

注意，把 5 个物品从 $u \Rightarrow v$ 又把 2 个物品从 $v \Rightarrow u$ 等价于把 $3$ 个物品从 $u \Rightarrow v$

这样规定 $f (u, v)$ 和 $f (v, u)$ 中最多只有一个正数，或者都为 $0$ ，且 $f (u, v) = - f (v, u)$

我们很容易发现几个性质：

容量限制 $f (u, v) \leq c (u, v)$
斜对称性 $f (u, v) = - f (v, u)$
流量平衡对于除了 $s$ 和 $t$ 之外的节点 $u$ ， $\sum f (u, v) = 0$

我们的目标是最大化 $| f | = \sum f (s, v) = \sum f (u, t)$

增广路算法

那么如何解决网络流问题呢？一种算法思想很简单，从 0 流开始不断增加流量。

外面计算每一条边上容量与流量之差（称为残余容量，简称残量），得到了一个残量网络。例如 $c = 16, f = 11$ 得到了残量就是 $16 - 11 = 5$ 和 $0 - (- 11) = 11$

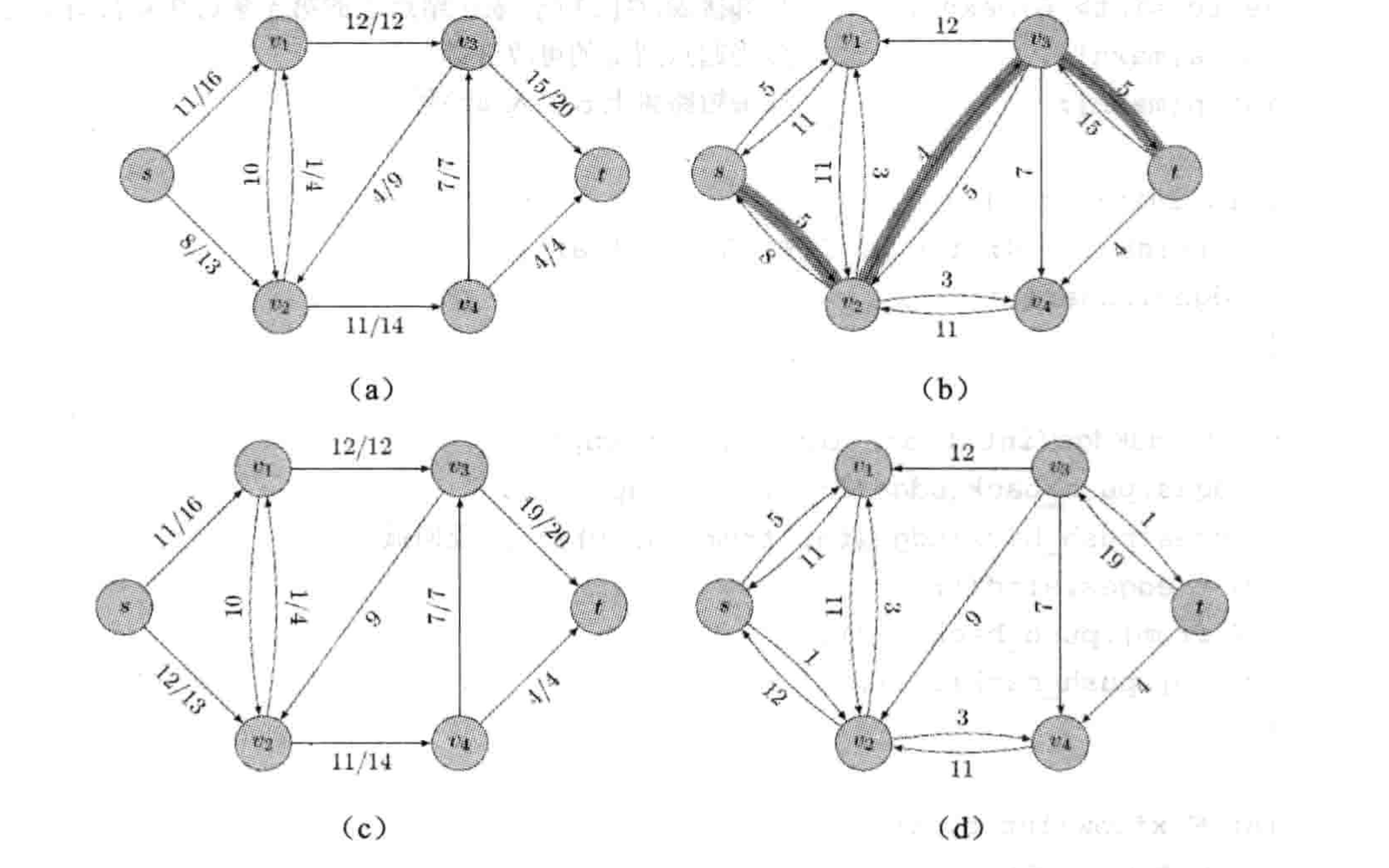
残量网络中任何一条从 $s$ 到 $t$ 的有向道路都对应一条原图中的增广路，只需要求出道路中所有残量的最小值 $d$ ，把对应边的流量都增加 $d$ 即可，这个过程称为增广。不难验证，如果增广前的流量的满足那 $3$ 个条件，增广后也满足。如果残量网络中不存在增广路，则当前流就是最大流。着就是著名的增广路定理。

Edmonds-Karp 算法

"找任意路径"最简单的方法是用 DFS，但是可以造数据把 DFS 卡死，所以我们使用 BFS 来找到一条增广路，这就是 Edmonds-Karp 算法。

相当于，我要找到一条从起点到终点的通路，且这条路上都要满足 $c a p \geq f l o w$ ，那么这次增广多出来的流量就是路径上差值的最小值

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int INF = 0x3f3f3f3f;
struct EdmondsKarp {
    int n, m; // n 为点数，m 为边数
    struct Edge {
        int from, to, cap, flow; // 起点，终点，容量，流量
    };

    vector<Edge> edges; // 边表。edges[e] 和 edges[e^1] 互为反向边
    vector<vector<int>> g; // 邻接表，G[i][j] 表示节点 i 的第 j 条边在 edges 中的序号

    void init (int n_) {
        n = n_; edges.clear();
        g.assign(n, vector<int>());
    }

    void add_e (int from, int to, int cap) {
        edges.push_back(Edge{from, to, cap, 0});
        edges.push_back(Edge{to, from, 0, 0});
        m = edges.size();
        g[from].push_back(m - 2);
        g[to].push_back(m - 1);
    }

    int max_flow (int s, int t) {
        int flow = 0;
        vector<int> a, pre (n, 0); // a 为当前节点到源点的可改进量, pre 为当前节点的前驱的边的编号
        while (true) {
            a.assign(n, 0);
            queue<int> q; q.push(s); a[s] = INF;
            while (!q.empty()) {
                int x = q.front(); q.pop();
                for (auto i : g[x]) {
                    Edge &e = edges[i];
                    if (a[e.to] == 0  && e.cap > e.flow) { // 未访问过且残留网络中有剩余容量
                        pre[e.to] = i;
                        a[e.to] = min(a[x], e.cap - e.flow); // 更新到源点的可改进量
                        q.push(e.to);

                    }
                }
                if (a[t]) break; // 已经找到增广路
            }
            if (a[t] == 0) break; // 没有增广路
            for (int u = t; u != s; u = edges[pre[u]].from) { // 从汇点向源点更新流量
                edges[pre[u]].flow += a[t];
                edges[pre[u] ^ 1].flow -= a[t];
            }
            flow += a[t];
        }
        return flow;
    }
};

struct Dinic {
    struct Edge {
        int from, to, cap, flow;
    };
    int n, m, s, t;
    vector<Edge> edges;
    vector<vector<int>> g;
    vector<int> d, cur; // d 为层次，cur 为当前弧优化

    void init (int n_) {
        n = n_; edges.clear();
        g.assign(n, vector<int>());
    }
};

signed main() {
    freopen ("P3376.in", "r", stdin);
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m, s, t; cin >> n >> m >> s >> t;
    EdmondsKarp ek; ek.init(n + 1);
    for (int i = 0; i < m; i++) {
        int u, v, c; cin >> u >> v >> c;
        ek.add_e(u, v, c);
    }
    cout << ek.max_flow(s, t) << '\n';
    return 0;
}

以上代码中，每条弧和他的反向弧保存在一起，且一个是奇数，一个是偶数，所以边 $i$ 的反向边为 i^1

在 BFS 的时候，时刻记下从 $s$ 到每个节点的路径上的最小残量 $a [i]$ ，所以 $a [t]$ 就是整条 $s - t$ 道路上的最小残量。

Dinic 算法

可以证明每次沿着最短增广路进行增广，这样最多需要 $O (n m)$ 次增广，因此算法的时间复杂度取决于找最短增广路的效率。

Edmonds-Karp 算法使用 BFS 来进行查找，需要 $O (m)$ 的时间，所以总时间复杂度来到 $O (n m^{2})$ ，有很大的提示空间。

Dinic 算法，宏观上讲，就是不停的用 BFS 构造层次图，然后用阻塞流来增广。

什么是层次图？在残量网络中，起点到结点 $u$ 的距离为 $d i s t (u)$ ，其中 $d i s t (u)$ 就可以看成是节点 $u$ 的层次。只保留每个节点出发到下一个层次的弧，得到的图就叫层次图。层次图上的任意路径都是 "起点 $\to$ 层次1 $\to$ 层次2 $\to$ 层次3 $\to$ ..." 每条这样的路径都是最短路

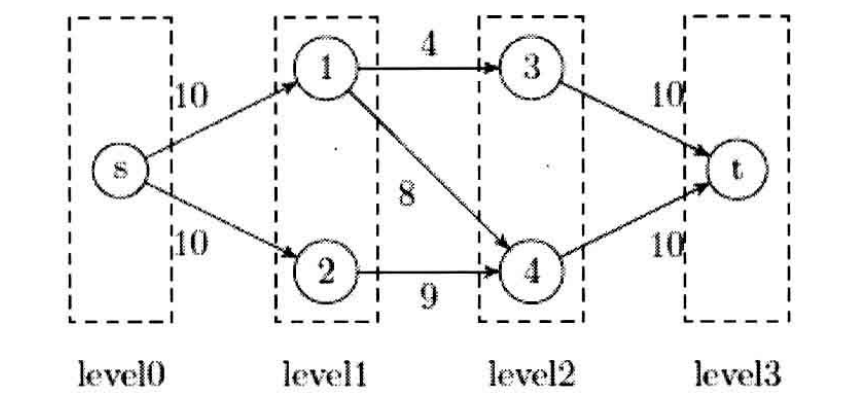
阻塞流是什么？实际上就是不考虑反向弧的极大流。

对应到程序里面就是从起点开始，在层次图中 DFS，每找到一条路就增广。

下面是 3 次增广的过程

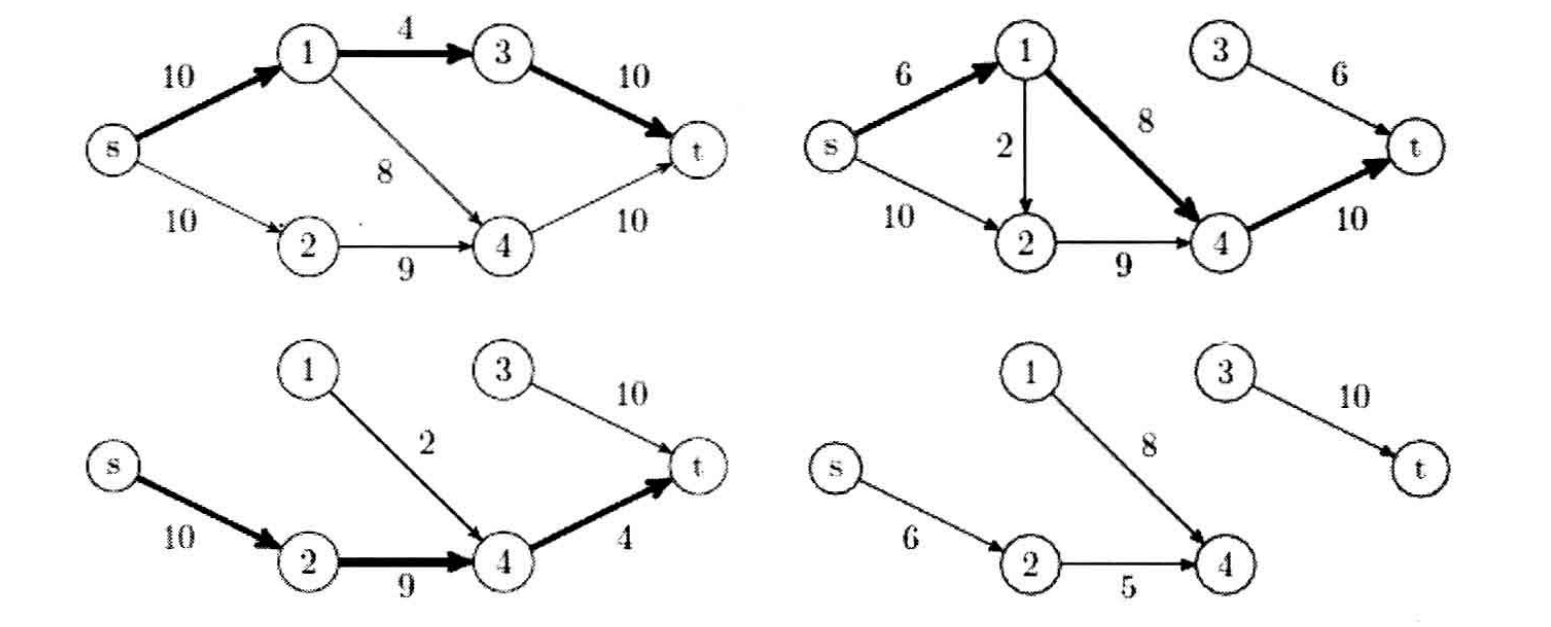
这 3 次增广后，层次图中不存在 $s - t$ 的路径，这三次增广流合成阻塞流

尽管在上文中我们仅在单条增广路上定义了增广/增广流，广义地，「增广」一词不仅可以用于单条路径上的增广流，也可以用于若干增广流的并——后者才是我们定义阻塞流时使用的意义。

实现过程如下：

在原图上 BFS 出分层图
在分层图中 DFS 出阻塞流 $f_{b}$
将 $f_{b}$ 并到原先的流 $f$ 中
重复以上过程直到不存在从 $s$ 到 $t$ 的路径

此时的 $f$ 即为最大流

当前弧优化

注意到，在分层图上 DFS 的过程中，如果节点 $u$ 同时具有大量入边和出边， $u$ 每次接受来自入边流入的流量时都遍历出边表来决定将流量传递给哪条出边，则 $u$ 这个局部的时间复杂度最坏可达 $O (| E |^{2})$ ，为了避免这一缺陷，如果每一时刻我们已经知道边 $(u, v)$ 已经增广到极限（边 $(u, v)$ 无剩余容量或 $v$ 后侧已增广至阻塞），则 $u$ 的流量没有必要再尝试流向出边 $(u, v)$ 。据此，对于每个节点 $u$ ，我们维护 $u$ 的出边表中第一条还有必要尝试的出边。我们称维护的这个指针为当前弧，称这个做法为当前弧优化。

复杂度

可以证明，Dinic 的时间复杂度为 $O (m i n (n^{2 / 3}, m^{1 / 2}) m)$ 。对于二分图最大匹配这样的特殊图，Dinic 的复杂度为 $O (n^{1 / 2} m)$

struct Dinic {
    struct Edge {
        int from, to, cap, flow;
    };
    int n, m, s, t;
    vector<Edge> edges;
    vector<vector<int>> g;
    vector<int> d, cur; // d 为层次，cur 为当前弧优化

    void init (int n_) {
        n = n_; edges.clear();
        d.assign(n, 0);
        g.assign(n, vector<int>());
    }

    void add_e (int from, int to, int cap) {
        edges.push_back(Edge{from, to, cap, 0});
        edges.push_back(Edge{to, from, 0, 0});
        m = edges.size();
        g[from].push_back(m - 2);
        g[to].push_back(m - 1);
    }

    bool bfs () {
        vector<int> vis (n, 0);
        queue<int> q; q.push(s); d[s] = 0; vis[s] = 1;
        while (!q.empty()) {
            int x = q.front(); q.pop();
            for (auto i : g[x]) {
                Edge &e = edges[i];
                if (vis[e.to] == 0 && e.cap > e.flow) {
                    vis[e.to] = 1;
                    d[e.to] = d[x] + 1;
                    q.push(e.to);
                }
            }
        }
        return vis[t]; // 是否存在能到达汇点的路径
    }

    int dfs (int x, int a) { // a 表示从源点到 x 的可改进量
        if (x == t || a == 0) return a;
        int flow = 0, f;
        for (int &i = cur[x]; i < g[x].size(); i++) { // 当前弧优化，在 cur[x] 之前都没有增广成功
            Edge &e = edges[g[x][i]];
            if (d[x] + 1 == d[e.to] && (f = dfs(e.to, min(a, e.cap - e.flow))) > 0) {
                e.flow += f;
                edges[g[x][i] ^ 1].flow -= f;
                flow += f;
                a -= f;
                if (a == 0) break;
            }
        }
        return flow;
    }

    int max_flow (int s, int t) {
        this->s = s; this->t = t;
        int flow = 0;
        while (bfs()) {
            cur.assign(n, 0);
            flow += dfs(s, INF);
        }
        return flow;
    }
};

signed main() {
    freopen ("P3376.in", "r", stdin);
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m, s, t; cin >> n >> m >> s >> t;
    Dinic ek; ek.init(n + 1);
    for (int i = 0; i < m; i++) {
        int u, v, c; cin >> u >> v >> c;
        ek.add_e(u, v, c);
    }
    cout << ek.max_flow(s, t) << '\n';
    return 0;
}

牛客的一道题，这样就能求出最小割的边集了

#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;

struct Dinic {
    struct Edge {
        int from, to, cap, flow;
    };
    int n, m, s, t;
    vector<Edge> edges;
    vector<vector<int>> g;
    vector<int> d, cur;

    void init(int n_) {
        n = n_; edges.clear();
        d.assign(n, 0);
        g.assign(n, vector<int>());
    }

    void add_e(int from, int to, int cap) {
        edges.push_back({from, to, cap, 0});
        edges.push_back({to, from, 0, 0});
        m = edges.size();
        g[from].push_back(m - 2);
        g[to].push_back(m - 1);
    }

    bool bfs() {
        fill(d.begin(), d.end(), -1);
        queue<int> q; q.push(s); d[s] = 0;
        while (!q.empty()) {
            int x = q.front(); q.pop();
            for (auto i : g[x]) {
                Edge &e = edges[i];
                if (d[e.to] == -1 && e.cap > e.flow) {
                    d[e.to] = d[x] + 1;
                    q.push(e.to);
                }
            }
        }
        return d[t] != -1;
    }

    int dfs(int x, int a) {
        if (x == t || a == 0) return a;
        int flow = 0, f;
        for (int &i = cur[x]; i < g[x].size(); i++) {
            Edge &e = edges[g[x][i]];
            if (d[x] + 1 == d[e.to] && (f = dfs(e.to, min(a, e.cap - e.flow))) > 0) {
                e.flow += f;
                edges[g[x][i] ^ 1].flow -= f;
                flow += f;
                a -= f;
                if (a == 0) break;
            }
        }
        if (flow == 0) d[x] = -1; // 表示从 x 出发找不到增广路
        return flow;
    }

    int max_flow(int s, int t) {
        this->s = s; this->t = t;
        int flow = 0;
        while (bfs()) {
            cur.assign(n, 0);
            flow += dfs(s, INF);
        }
        return flow;
    }
};

int main() {
    int n, m, k; cin >> n >> m >> k;
    Dinic dinic; dinic.init(2 * n * k + 2); int S = 0, T = 2 * n * k + 1;

    auto get_id = [&] (int x, int j, int op) {
        return (x - 1) * k * 2 + j * 2 + op + 1;
    };

    auto inv_id = [&] (int id) {
        id--; int x = (id - 1) / 2 / k + 1, j = (id - 1) / 2 % k, op = (id - 1) % 2;
        return x;
    };
    
    vector<vector<int>> g(n + 1);
    vector<int> du_in(n + 1), du_out(n + 1);
    for (int i = 1; i <= m; i++) {
        int u, v; cin >> u >> v;
        g[u].push_back(v);
        du_out[u]++; du_in[v]++;
    }

    for (int i = 1; i <= n; i++) {
        if (du_in[i] == 0 || du_out[i] == 0) {
            if (du_in[i] == 0) dinic.add_e(S, get_id(i, 0, 1), INF);
            if (du_out[i] == 0) dinic.add_e(get_id(i, k - 1, 0), T, INF);
        }
        else {
            for (int j = 0; j < k; j++) {
                dinic.add_e(get_id(i, j, 0), get_id(i, j, 1), 1);
                if (j + 1 < k) dinic.add_e(get_id(i, j, 0), get_id(i, j + 1, 1), INF);
            }
        }

        int u = i;
        for (auto v : g[u]) {
            for (int j = 0; j < k; j++)
                dinic.add_e(get_id(u, j, 1), get_id(v, j, 0), INF);
        }
    }

    auto siz = dinic.max_flow(S, T);
    if (siz > n) {
        cout << -1 << '\n';
        return 0;
    }
    cout << siz << '\n';
    vector<int> ans;
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j < k; j++) {
            if(dinic.d[get_id(i, j, 0)] != -1 && dinic.d[get_id(i, j, 1)] == -1) {
                // 说明断了 i 这个点
                ans.push_back(i);
            }
        }
    }
    for (auto x : ans) cout << x << ' ';
    return 0;
}

最小割

有一个与最大流关系密切的问题，最小割。

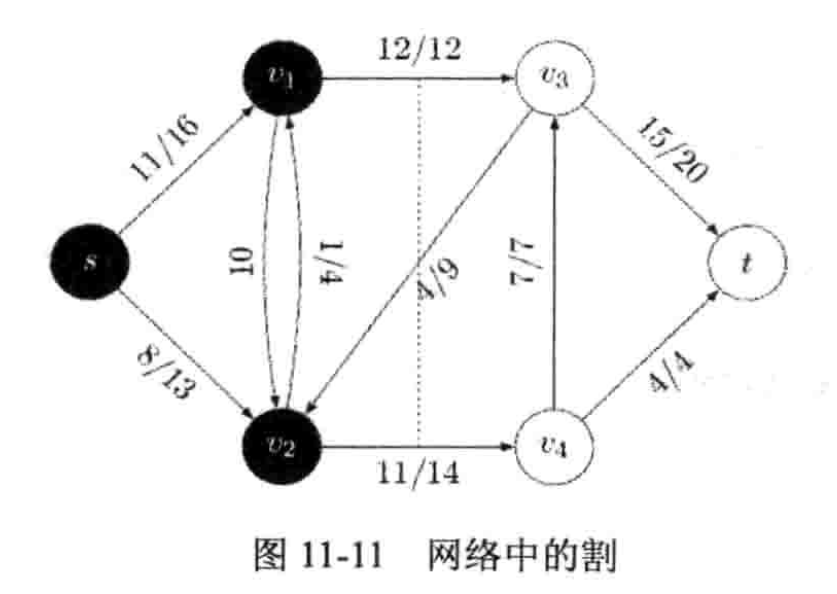
把所有的顶点分成两个集合 $S, T$ ，其中源点 $s$ 在 $S$ 中，汇点 $t$ 在集合 $T$ 中。图中黑色的点属于 $S$ ，白色的点属于 $T$ 。

如果把起点在 $S$ 中，终点在 $T$ 中的边全部删除，那么这个图就被分成了两部分 $s$ 无法到达 $t$ ，这样的集合划分 $(S ， T)$ 称为一个 $s - t$ 割

它的容量定义为 $c (S, T) = \sum_{w \in S, v \in T} C (u, v)$ ，即起点在 $S$ 中，终点在 $T$ 中的所有边的容量和

最小割就是求得一个割 $(S, T)$ ，使得割的容量 $c (S, T)$ 最小

最小割最大流定理

可以从另外一个角度来看待割，从 $s$ 运送到 $t$ 的物品必然通过跨越 $S$ 和 $T$ 的边，所以从 $s$ 到 $t$ 的净流量等于 $| f | = f (S, T) = \sum_{w \in S, v \in T} f (u, v) \leq \sum_{w \in S, v \in T} c (u, v) = c (S, T)$

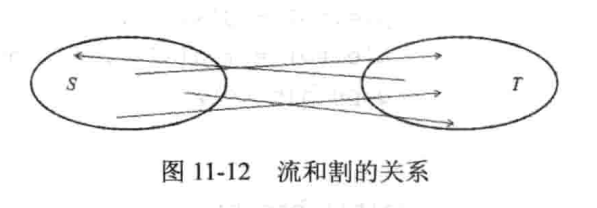
注意这里的割是任取的，因此我们得到了一个重要结论，对于任意 $s - t$ 流 $f$ 和任意 $s - t$ 割 $(S, T)$ 有 $| f | \leq c (S, T)$

在残量网络中若不存在增广路，那么说明残量网络中 $s$ 和 $t$ 并不连通。当 BFS 没有找到任何 $s - t$ 道路时，把已标号节点（ $(a [u]) > 0$ 的节点）看成集合 $S$ ，另外的节点看成 $T$ ，则在残量网络中 $S$ 和 $T$ 分离，因此在原图中跨越 $S$ 和 $T$ 的弧全部满载，且没有 $T$ 回到 $S$ 的流量，因此这种情况下 $| f | = c (S, T)$ 。所以在增广路算法结束时， $f$ 是 $s - t$ 的最大流， $(S, T)$ 是 $s - t$ 的最小割，且最大流 $=$ 最小割。

费用流

假设每条边除了有一个容量限制外，还有一个单位流量所需的费用（cost）。

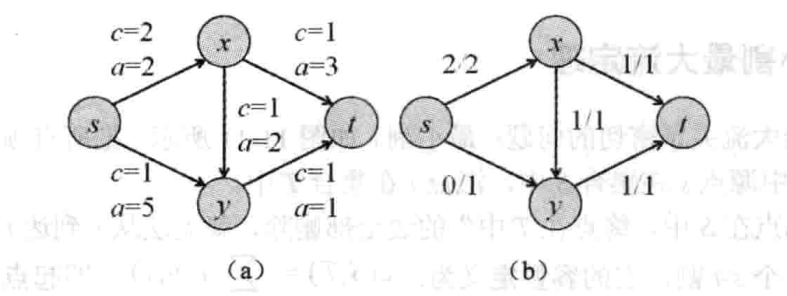
图中用 $a$ 表示费用， $c$ 表示容量。b 图给出了一个在总流量最大的前提下，总费用最小的流（费用为 10），即最小费用最大流。

SSP 算法

SSP（Successive Shortest Path）算法是一个贪心的算法。它的思路是 每次寻找单位费用最小的增广路进行增广，直到图上不存在增广路为止。

什么时候单位费用最小？就是把费用看成距离，单位费用最小看成最短路

如果图上存在单位费用为负的圈，SSP 算法无法正确求出该网络的最小费用最大流。此时需要先使用消圈算法消去图上的负圈。

最小费用路算法，和 Edmonds-Karp ，Dinic 算法类似，但是每次用 Bellman-Ford 算法增广路，因为 Bellman-Ford 可以消去负权回路

贪心的思路：只要初始流是该流量下的最小费用可行流，每次增广后的新流都是新流量下的最小费用流。

基于 Edmonds-Karp 的实现

const int INF = 0x3f3f3f3f;
struct EdmondsKarp {
    struct Edge {
        int from, to, cap, flow, cost;
    };
    int n, m;
    vector<Edge> edges;
    vector<vector<int>> g;

    void init(int n_) {
        n = n_; edges.clear();
        g.assign(n, vector<int>());
    }

    void add_e (int from, int to, int cap, int cost) {
        edges.push_back(Edge{from, to, cap, 0, cost});
        edges.push_back(Edge{to, from, 0, 0, -cost});
        m = edges.size();
        g[from].push_back(m - 2);
        g[to].push_back(m - 1);
    }

    bool bellmon_ford (int s, int t, int &flow, int &cost) {
        vector<int> dis (n, INF), a(n, 0), pre(n, 0), vis(n, 0); 
        // dis 为源点到当前点的最短距离, a 为当前节点到源点的可改进量, pre 为当前节点的前驱的边的编号, vis 为当前节点是否在队列中
        queue<int> q; q.push(s); dis[s] = 0; a[s] = INF;
        while (!q.empty()) {
            int x = q.front(); q.pop();
            vis[x] = 0;
            for (auto i : g[x]) {
                Edge &e = edges[i];
                if (e.cap > e.flow && dis[e.to] > dis[x] + e.cost) {
                    dis[e.to] = dis[x] + e.cost;
                    pre[e.to] = i;
                    a[e.to] = min(a[x], e.cap - e.flow);
                    if (!vis[e.to]) {q.push(e.to); vis[e.to] = 1;}
                }
            }
        }
        if (dis[t] == INF) return false;
        flow += a[t]; cost += dis[t] * a[t]; // 更新流量和费用
        for (int u = t; u != s; u = edges[pre[u]].from) {
            edges[pre[u]].flow += a[t];
            edges[pre[u] ^ 1].flow -= a[t];
        }
        return true;
    }

    pair<int, int> min_cost_max_flow(int s, int t) { // 返回最大流和最小费用
        int flow = 0, cost = 0;
        while (bellmon_ford(s, t, flow, cost));
        return {flow, cost};
    }
};

int main() {
    freopen ("P3381.in", "r", stdin);
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int n, m, s, t; cin >> n >> m >> s >> t;
    EdmondsKarp ek; ek.init(n + 1);
    for (int i = 0; i < m; i++) {
        int u, v, c, w; cin >> u >> v >> c >> w;
        ek.add_e(u, v, c, w);
    }
    auto [flow, cost] = ek.min_cost_max_flow(s, t);
    cout << flow << ' ' << cost << '\n';
    return 0;
}

基于 Dinic 的代码实现

struct Dinic {
    int n, m, s, t;
    struct Edge {
        int from, to, cap, flow, cost;
    };
    vector<Edge> edges;
    vector<vector<int>> g;
    vector<int> d, cur, vis;

    void init(int n_) {
        n = n_; edges.clear();
        g.assign(n, vector<int>());
        d.resize(n); cur.resize(n); vis.resize(n);
    }

    void add_e(int from, int to, int cap, int cost) {
        edges.push_back(Edge{from, to, cap, 0, cost});
        edges.push_back(Edge{to, from, 0, 0, -cost});
        m = edges.size();
        g[from].push_back(m - 2);
        g[to].push_back(m - 1);
    }

    bool bellman_ford () {
        fill (d.begin(), d.end(), INF);
        fill (vis.begin(), vis.end(), 0);
        queue<int> q; q.push(s); d[s] = 0; vis[s] = 1;
        while (!q.empty()) {
            int x = q.front(); q.pop();
            vis[x] = 0;
            for (auto i : g[x]) {
                Edge &e = edges[i];
                if (e.cap > e.flow && d[e.to] > d[x] + e.cost) {
                    d[e.to] = d[x] + e.cost;
                    if (!vis[e.to]) {q.push(e.to); vis[e.to] = 1;}
                }
            }
        }
        return d[t] != INF;
    }

    int dfs (int x, int a) {
        if (x == t || a == 0) return a;
        int flow = 0, f;
        vis[x] = 1;
        for (int &i = cur[x]; i < g[x].size(); i++) {
            Edge &e = edges[g[x][i]];
            if (!vis[e.to] && d[x] + e.cost == d[e.to] && (f = dfs(e.to, min(a, e.cap - e.flow))) > 0) {
                e.flow += f; edges[g[x][i] ^ 1].flow -= f;
                flow += f;
                a -= f;
                if (a == 0) break;
            }
        }
        return flow;
    }

    pair<int, int> min_cost_max_flow(int s, int t) {
        this->s = s; this->t = t;
        int flow = 0, cost = 0;
        while (bellman_ford()) {
            fill(cur.begin(), cur.end(), 0);
            fill(vis.begin(), vis.end(), 0);
            while (int f = dfs(s, INF)) {
                flow += f;
                cost += f * d[t];
                fill(vis.begin(), vis.end(), 0);
            }
        }
        return {flow, cost};
    }
};

int main() {
    freopen ("P3381.in", "r", stdin);
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int n, m, s, t; cin >> n >> m >> s >> t;
    Dinic ek; ek.init(n + 1);
    for (int i = 0; i < m; i++) {
        int u, v, c, w; cin >> u >> v >> c >> w;
        ek.add_e(u, v, c, w);
    }
    auto [flow, cost] = ek.min_cost_max_flow(s, t);
    cout << flow << ' ' << cost << '\n';
    return 0;
}