15.圆相关计算

圆相关计算

圆的定义

圆上一点拥有唯一的圆心角，在定义圆的时候，可以加一个通过圆心角求坐标的函数

struct Circle {
    Point c;
    double r;
    Circle(Point c = Point(), double r = 0) : c(c), r(r) {}
    Point point(double a) { return Point(c.x + cos(a) * r, c.y + sin(a) * r); } // 通过圆心角求圆上的点
};

直线和圆的交点

假设直线为 $A B$ 圆的圆心为 $C$ ，半径为 $r$ 。

第一种方法就是解方程组。设交点为 $P = A + t (B - A)$ ，代入圆方程的整理后得到 $(a t + b)^{2} + (c t + d)^{2} = r^{2}$ ，进一步得到一元二次方程 $e t^{2} + f t + g = 0$ 根据判别式就可以判断是相离，相切，还是相交了

int line_circle_intersection(Point A, Point B, Circle C, vector<Point> &sol) {
    double a = B.x - A.x, b = A.x - C.c.x, c = B.y - A.y, d = A.y - C.c.y;
    double e = a * a + c * c, f = 2 * (a * b + c * d), g = b * b + d * d - C.r * C.r;
    double delta = f * f - 4 * e * g;
    if (dcmp(delta) < 0) return 0;
    if (dcmp(delta) == 0) {
        double t = -f / (2 * e);
        sol.push_back(Point(A.x + t * a, A.y + t * c));
        return 1;
    }
    double t1 = (-f - sqrt(delta)) / (2 * e), t2 = (-f + sqrt(delta)) / (2 * e);
    sol.push_back(Point(A.x + t1 * a, A.y + t1 * c));
    sol.push_back(Point(A.x + t2 * a, A.y + t2 * c));
    return 2;
}

两圆相交

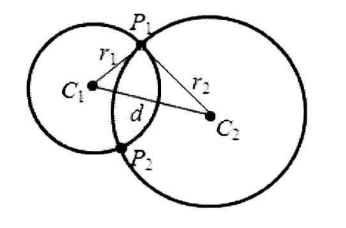
假定圆心分别为 $C_{1}, C_{2}$ 半径为 $r 1, r 2$ 圆心距为 $d$ ，通过余弦定理能算出 $C_{1}, C_{2}$ 到 $C_{1} P_{1}$ 的角 $d a$ 根据向量 $C 1 C 2$ 的极角 $a$ ，加减 $d a$ 就可以得到 $C_{1} P_{1}$ 和 $C_{1} P_{2}$ 的极角。有了极角，就可以很方便地计算出 $P_{1}$ 和 $P_{2}$ 的坐标了

//求两圆交点
double angle0(Vector v) { return atan2(v.y, v.x); } //求极角，注意不要错用 atan 了

int circle_circle_intersection(Circle C1, Circle C2, vector<Point> &sol) {
    double d = length(C1.c - C2.c);
    if (dcmp(d) == 0) {
        if (dcmp(C1.r - C2.r) == 0) return -1; // 重合
        return 0;
    }
    if (dcmp(C1.r + C2.r - d) < 0) return 0;  // 外离
    if (dcmp(fabs(C1.r - C2.r) - d) > 0) return 0;  // 内含
    double a = angle0(C2.c - C1.c); // C1 到 C2 的向量的极角
    double da = acos((C1.r * C1.r + d * d - C2.r * C2.r) / (2 * C1.r * d)); // 余弦定理
    Point p1 = C1.point(a - da), p2 = C1.point(a + da); // 两个交点
    sol.push_back(p1);
    if (p1 == p2) return 1;
    sol.push_back(p2);
    return 2;
}

过定点做圆的切线

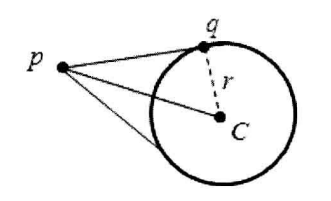
先求出 $p q$ 的距离， $p c$ 与 $p q$ 的夹角 $a n g$ ，则向量 $p c$ 的极角加减 $a n g$ 就是两条切线的极角

int tangents(Point P, Circle C, Vector* v) {
    Vector u = C.c - P;
    double dist = length(u);
    if (dist < C.r) return 0;
    if (dcmp(dist - C.r) == 0) {
        v[0] = rotate(u, PI / 2);
        return 1;
    }
    double ang = asin(C.r / dist);
    v[0] = rotate(u, -ang);
    v[1] = rotate(u, ang);
    return 2;
}

两圆的公切线

两个圆的公切线，根据两圆的圆心距从小到大排列，一共有 6 种情况

情况一：两圆完全重合。有无数条公切线。
情况二：两圆内含，没有公共点。没有公切线
情况三：两圆内切，有 $1$ 条外公切线
情况四：两圆相交，有 $2$ 条外公切线
情况五：两圆外切，有 $3$ 条公切线，其中一条内公切线，两条外公切线
情况六：两圆相离，有 $4$ 条公切线，其中两条内公切线，两条外公切线

可以根据圆心距和半径的关系辨别出这 $6$ 种情况

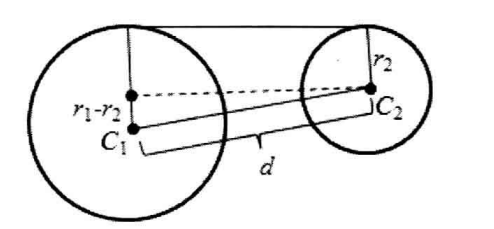
对于情况六种的内公切线

内切只需要用反三角函数求出 $C_{1} C_{2}$ 和 $r_{1}$ 的夹角 $a n g$ 就可以解决了

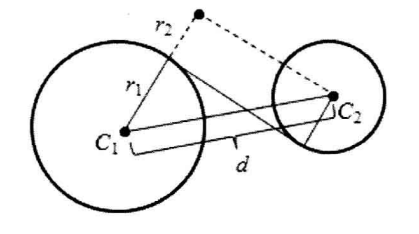
外切也是同理