10.二维计算几何基础

二维计算几何基础

定义向量

const double eps = 1e-10;

struct Point {
    double x, y;
    Point() {}
    Point(double x, double y) : x(x), y(y) {}
};

typedef Point Vector;

Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator - (Point A, Point B) { return Vector(A.x - B.x, A.y - B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x * p, A.y * p); }
Vector operator / (Vector A, double p) { return Vector(A.x / p, A.y / p); }

int dcmp(double x, double y = 0.0) { // 比较两个浮点数的大小
    if (fabs(x - y) < eps) return 0;
    return x < y ? -1 : 1;
}

bool operator == (const Point &a, const Point &b) {
    return dcmp(a.x, b.x) == 0 && dcmp(a.y, b.y) == 0;
}

基本运算

点积

$\vec{O A} \cdot \vec{O B} = x_{A} x_{B} + y_{A} y_{B}$

double dot(Vector A, Vector B) { return A.x * B.x + A.y * B.y; }

长度

double length(Vector A) { return sqrt(dot(A, A)); }

角度

两个向量中的角度可以使用点积计算

$c o s < A, B >= \frac{A \cdot B}{| A | | B |}$

double angle(Vector A, Vector B) { return acos(dot(A, B) / length(A) / length(B)); }

叉积

$\vec{O A} \times \vec{O B} = x_{A} y_{B} - x_{B} y_{A}$

可以使用右手螺旋法则判断正负

double cross(Vector A, Vector B) { return A.x * B.y - A.y * B.x; }

三角形面积

可以利用叉积计算

double area2(Point A, Point B, Point C) { return cross(B - A, C - A); }

向量旋转

$x^{'} = x \cos a - y \sin a, y^{'} = x \sin a + y \cos a$

[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} \cos x & - s i n x \\ \sin x & c o s x \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]

Vector rotate(Vector A, double rad) { // 逆时针旋转 rad 弧度
    return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
}

求单位法向量

Vector normal (Vector A) { // 左转 90 度， 单位法向量
    double L = length(A);
    return Vector(-A.y / L, A.x / L);
}

点和直线

直线可以用直线上一点 $P_{0}$ 和方向向量 $v$ 表示（虽然这个向量的大小没什么用处）。

直线上所有点 $P$ 满足 $P = P_{0} + t v$ 其中 $t$ 称为参数。如果已知直线上的两个不同点 $A, B$ 则方向向量为 $B - A$ ，所以参数方程为 $A + (B - A) t$

参数方程方便的地方在于直线，射线和线段的方程形式是一样的，区别仅仅在于参数

直线的 $t$ 没有范围限制，射线的 $t > 0$ ，线段的 $t$ 在 $0 \sim 1$ 之间

直线的定义

struct Line {
    Point P;
    Vector v;
    Line() {}
    Line(Point P, Vector v) : P(P), v(v) {}
    Point point(double t) { return P + v * t; }
}

直线交点

设直线分别为 $P + t v$ 和 $Q + t w$ ，设向量 $\vec{u} = Q P$ ，交点在第一条直线的参数为 $t_{1}$ ，第二条直线上的参数为 $t_{2}$ 则 $x$ 和 $y$ 坐标可以列出一个方程，解得

t_{1} = \frac{c r o s s (w, u)}{c r o s s (v, w)}, t_{2} = \frac{c r o s s (v, u)}{c r o s s (v, w)}

代码如下，调用前请确保两条直线有唯一交点，当且仅当 $C r o s s (v, w) \neq 0$

Point line_intersection(Point P, Vector v, Point Q, Vector w) {
    Vector u = P - Q;
    double t = cross(w, u) / cross(v, w);
    return P + v * t;
}

Point line_intersection(Line a, Line b) {
    Vector u = a.P - b.P;
    double t = cross(b.v, u) / cross(a.v, b.v);
    return a.point(t);
}

点到直线的距离

用叉积算出，用平行四边形的面积除以底

double distance_to_line(Point P, Point A, Point B) {
    Vector v1 = B - A, v2 = P - A;
    return fabs(cross(v1, v2) / length(v1));
}

double distance_to_line(Point P, Line l) {
    Vector v1 = l.v, v2 = P - l.P;
    return fabs(cross(v1, v2) / length(v1));
}

点到线段的距离

点到线段的距离有两种可能

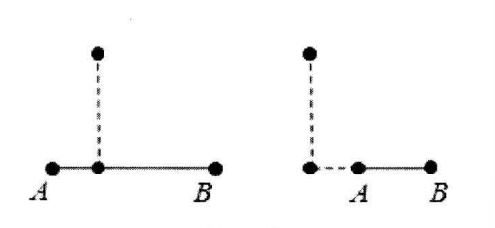
如果投影点为 $Q$ 在线段 $A B$ 上，则所求距离就是 $P$ 点直线 $A B$ 的距离(左图)，如果在射线 $B A$ 上，则所求距离为 $Q A$ ，如果在射线 $A B$ 上，则所求距离为 $Q B$

判断 $Q$ 的位置建议用点积确定

double distance_to_segment(Point P, Point A, Point B) {
    if (A == B) return length(P - A);
    Vector v1 = B - A, v2 = P - A, v3 = P - B;
    if (dcmp(dot(v1, v2)) < 0) return length(v2);
    if (dcmp(dot(v1, v3)) > 0) return length(v3);
    return fabs(cross(v1, v2)) / length(v1);
}

点在直线上的投影

我们把直线 $A B$ 写成参数式 $A + t v$ （ $v$ 为向量 $A B$ ）且设 $Q$ 的参数为 $t_{0}$ 那么 $Q = A + t_{0} v$ 根据 $P Q$ 垂直于 $A B$ ，两个向量的点积应该为 $0$ ，可以得出 $v \cdot (P - (A + t_{0} v)) = 0$ 根据分配律有 $v \cdot (P - A) - t_{0} \cdot (v \cdot v) = 0$ 就能解出 $t_{0}$ 了

Point line_projection(Point P, Point A, Point B) {
    Vector v = B - A;
    return A + v * (dot(v, P - A) / dot(v, v));
}

线段相交判定

我们定义两条线段相交的充要条件是，每条线段的两个端点都在另一条线段的两侧(叉积的符号不同)，不包括在端点处相交（这种方法不能判断在端点处相交）

bool is_segment_proper_intersection(Point a1, Point a2, Point b1, Point b2) {
    double c1 = cross(a2 - a1, b1 - a1), c2 = cross(a2 - a1, b2 - a1),
           c3 = cross(b2 - b1, a1 - b1), c4 = cross(b2 - b1, a2 - b1);
    return dcmp(c1) * dcmp(c2) < 0 && dcmp(c3) * dcmp(c4) < 0;
}

如果允许在端点处相交

如果 $c_{1}, c_{2}$ 都是 $0$ , 表示两线段共线
如果 $c_{1}, c_{2}$ 不都是 $0$ ,则只有一种相交方法，即某个端点在另外一条线段上，为了判断上述情况是否发生，还需要如下一段代码判断一个点是否在一条线段上(不包含端点)

bool is_point_on_segment(Point P, Point A, Point B) {
    return dcmp(cross(A - P, B - P)) == 0 && dcmp(dot(A - P, B - P)) <= 0; // <= 0 保证端点也算，< 0 不算
}

多边形

把多边形从第一个顶点出发把凸多边形分成 $n - 2$ 个三角形，然后把面积加起来

其实这个方法对非凸多边形也适用，因为三角形的面积是有向的，在外面的部分可以抵消掉

多边形面积

double convex_polygon_area(vector<Point> &p) {
    int n = p.size();
    double area = 0;
    for (int i = 1; i < n - 1; i++) area += area2(p[0], p[i], p[i + 1]);
    return area / 2;
}

点在多边形内判定

我们定义一个多边形就是二维平面上被一系列首尾相连，闭合的折线段围成的区域，在程序种一般用顶点数组表示，各个点按逆时针顺序排列

有两种方法能判定

第一种是射线法

从某个判定点出发，任意引一条射线，如果和边界相交奇数次，说明在多边形内，如果相交都数次，说明在多边形外。不能再端点处和完整边处相交

第二种是转角度法

我们把多边形每条边转的角度加起来，如果是 360° 说明再多边形内，如果是 0°，说明再多边形外，如果是 180° 说明在多边形的边界上

一般我们使用第二种方法，直接按照定义去实现需要计算大量的反三角函数，容易产生精度问题。我们一般假象一条向右的射线，统计多边形穿过这条射线正反多少次，把这个记为绕数 $c n t$ ，逆时针穿过时， $c n t + 1$ ，顺时针穿过时 $c n t - 1$

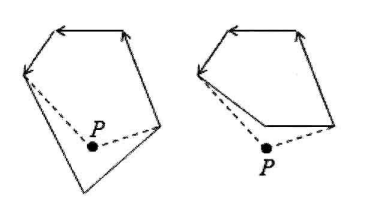
bool is_point_in_polygon(Point p, vector<Point> &poly) {
    int n = poly.size(), cnt = 0;
    for (int i = 0; i < n; i++) {
        Point u = poly[i], v = poly[(i + 1) % n];
        if (is_point_on_segment(p, u, v)) return true;
        double k = cross(v - u, p - u);
        double d1 = dcmp(u.y - p.y), d2 = dcmp(v.y - p.y);
        if (k > 0 && d1 <= 0 && d2 > 0) cnt++;
        if (k < 0 && d2 <= 0 && d1 > 0) cnt--;
    }
    return cnt != 0; // 0 外部，1 内部
}