RMQ

ST表

ST 表基于倍增思想，可以做到 $O(n\log n)$ 预处理，$O(1)$ 回答每个询问。来处理区间最大值或者区间 gcd 问题，但是不支持修改操作

定义 $f[i][j]$ 表示区间 $[i,i+2^j-1]$ 的最大值，显然 $f(i,0)=a_i$

根据定义式，第二维就相当于倍增的时候跳了 $2^j-1$ 步

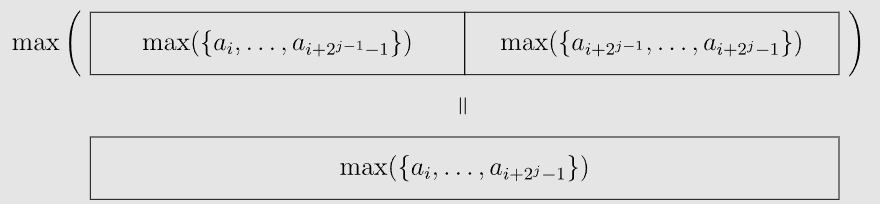
所以预处理的转移方程自然而然就可以得出了：

对于每个询问 $[l,r]$ 我们分成两部分：$[l,l+2^s-1]$ 与 $[r-2^s+1,r]$，其中 $s=\lfloor {\log }_2(r-l+1)\rfloor$

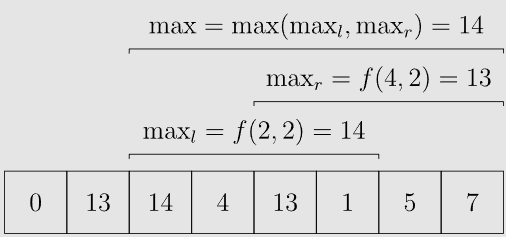
#include <bits/stdc++.h>
using namespace std;
int main() {
    freopen ("P3865.in", "r", stdin);
    int n, m; cin >> n >> m;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    vector<vector<int> > f(n + 1, vector<int>(20));
    vector<int> lg2(n + 1, 0);
    for (int i = 1; i <= n; i++)
        f[i][0] = a[i];
    for (int i = 2; i <= n; i++)
        lg2[i] = lg2[i >> 1] + 1;
    for (int j = 1; j < 20; j++)
        for (int i = 1; i + (1 << j) - 1 <= n; i++)
            f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
    auto query = [&] (int l, int r) {
        int s = lg2[r - l + 1];
        return max(f[l][s], f[r - (1 << s) + 1][s]);
    };
    while (m--) {
        int l, r; cin >> l >> r;
        cout << query(l, r) << '\n';
    }
    return 0;
}