90.笛卡尔树

Treap 树的每个节点有两个属性，键值和优先级

笛卡尔树是一种特殊的，简化的 Treap，它的每个节点的键值预先给定，但是优先级预先给定或者随机生成

笛卡尔树主要用于处理一个确定的数列，数列中的一个数有两个属性，在数列中的位置、数值。把位置看成键值，把数值看成优先级

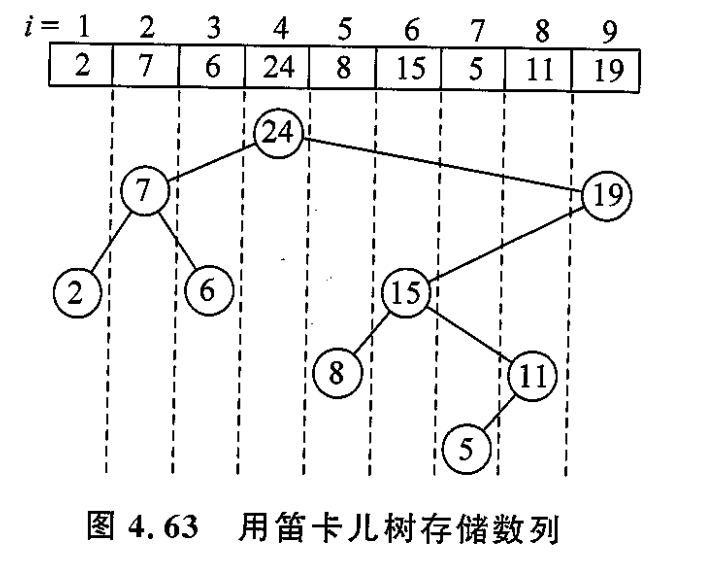
根据这个数列构造出来的笛卡尔树符合 Treap 树的两个特征

1. 以每个数的位置为键值，它是一颗 BST。也就是说，对这棵树左中序遍历，返回的就是数列
2. 把数值看作 Treap 树的优先级，把数列建成一个堆。如果按大根堆建这颗树，那么在每个子树上，子树的根的权值是整棵子树上最大的

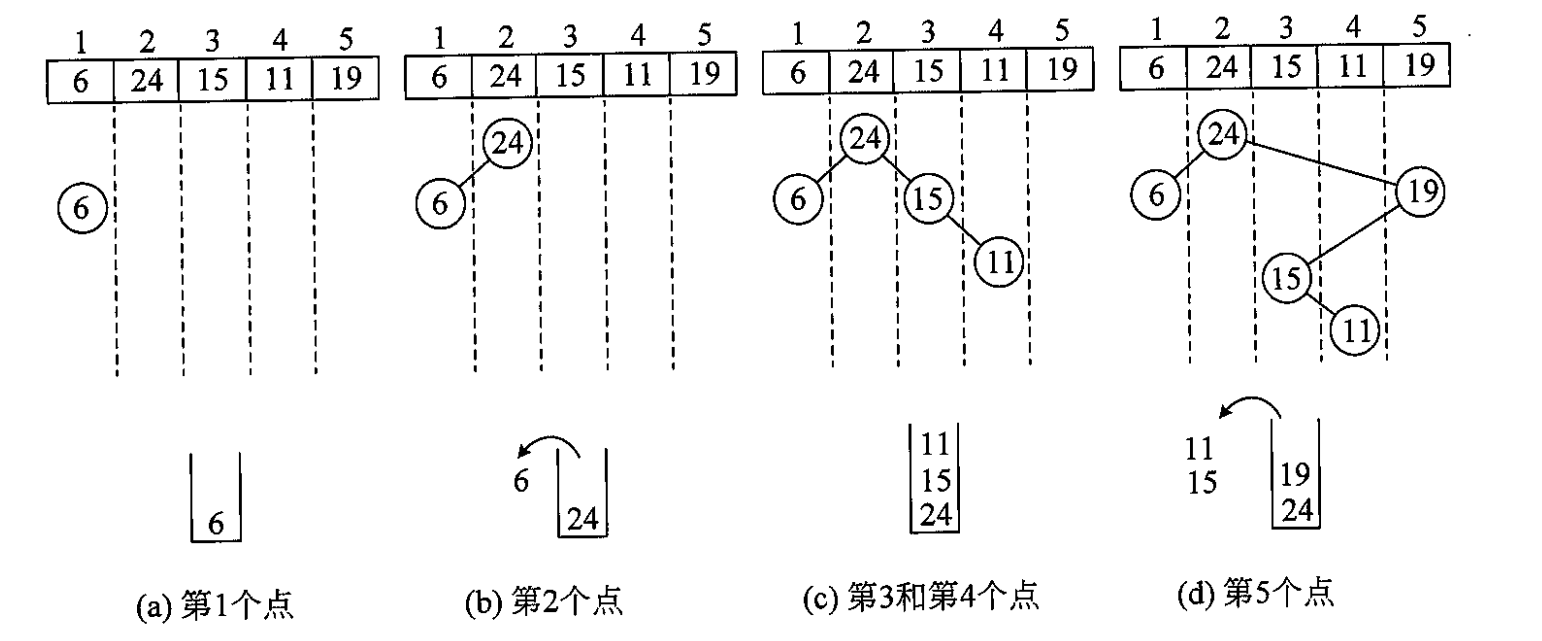
用单调栈建笛卡尔树

笛卡尔树存在 $O(n)$ 的建树方法，考虑使用单调栈

每次插入新的节点，横向的位置是固定的，思考新的节点的纵向位置，只需要考虑新的节点插在最右端的哪个位置，着很容易用一个单调栈来实现

维护一个单调减的单调栈，如果新加入的节点比原来的节点小，那么按照大根堆的性质，新的节点就是栈顶节点的右儿子，如果比栈顶的节点小，就找到一个比新加入节点大的点，然后成为这个点的右儿子，新加入点的左儿子是最后一个出栈的点

#include <cstdio>
#include <cstring>
#include <string>
#include <vector>
#include <stack>
#include <algorithm>

using namespace std;
const int INF = 2e9;
const int maxn = 1e5 +7;
struct Node{
    char s[115];
    int ls,rs,pri;
}t[maxn];

int n;

void build(){
    stack<int> st; st.push(0); //t[0].pri = INF;
    for(int i=1;i<=n;i++){
        int pos=st.top();
        while(!st.empty() && t[pos].pri < t[i].pri){ // 如果栈顶元素的优先级比当前元素的优先级小，那么就一直往上找，直到找到一个优先级比当前元素大的元素
            st.pop();
            pos = st.top();
        }
        t[i].ls = t[pos].rs;
        t[pos].rs = i;
        st.push(i);
    }
}

void inorder(int x){
    if(x == 0) return;
    printf("(");inorder(t[x].ls);
    printf("%s/%d",t[x].s,t[x].pri);
    inorder(t[x].rs);printf(")");
}

bool cmp(Node a,Node b){
    return strcmp(a.s,b.s) < 0;
}

int main(){
    freopen("1785.in","r",stdin);
    freopen("1785.out","w",stdout);
    while(scanf("%d",&n)!=EOF&&n){
        for(int i=1;i<=n;i++){
            t[i].ls=t[i].rs=0;
            scanf(" %[^/]/%d",t[i].s,&t[i].pri);
        }
        t[0].ls=t[0].rs=0; t[0].pri = INF;
        sort(t+1,t+n+1,cmp);
        build();
        inorder(t[0].rs);
        printf("\n");
    }
    return 0;
}