80.树分治
树分治
点分治
点分治是一种思想,通常需要配合其他算法来达到目的
实现
类似于 cdq 分治思想,我们对于树上的点对问题,把树按照重心分治,先考虑不同子树之间对于答案的影响,然后递归处理其子树
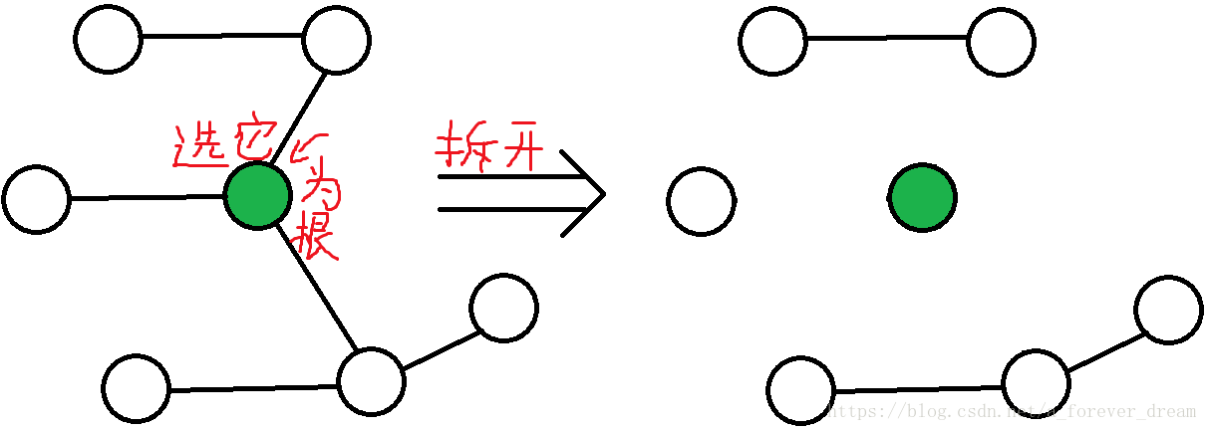
使用一次 dfs 找到树的重心
function<int(int)> get_root = [&] (int u) -> int{
int res = 0;
int rt = u;
function<void(int, int)> get_siz = [&] (int u, int fa) {
siz[u] = 1;
for (auto [v, w] : g[u]) {
if (v == fa || vis[v]) continue;
get_siz(v, u);
siz[u] += siz[v];
}
};
function<void(int, int)> dfs = [&] (int u, int fa) {
max_son[u] = 0;
for (auto [v, w] : g[u]) {
if (v == fa || vis[v]) continue;
dfs(v, u);
max_son[u] = max(max_son[u], siz[v]);
}
max_son[u] = max(max_son[u], siz[rt] - siz[u]);
if (res == 0 || max_son[u] < max_son[res])
res = u;
};
get_siz(u, 0);
dfs(u, 0);
return res;
};
我这里多用了一次 dfs 来获得这个子树的大小(在后面求重心的时候需要用),但实际上这个可以预处理出来
这里我用一道例题来讲解点分治
给定一颗有
个点的树,询问树上距离为 的点对是否存在
暴力求解是
我们考虑如何求一个以 calc(u)
首先找到这颗子树的重心记作
那么 solve(root) 怎么写呢,需要构造
但是这里可以会把在同一棵子树的点对也计算上,根据容斥原理,枚举每个子树,把子树内重复计算的部分减去就好了
计算好通过
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
freopen ("P3806.in", "r", stdin);
freopen ("P3806.out", "w", stdout);
ios::sync_with_stdio(false);
int n, m; cin >> n >> m;
vector<vector<pair<int, int>>> g(n + 1);
for (int i = 1; i < n; i++) {
int u, v, w; cin >> u >> v >> w;
g[u].push_back({v, w});
g[v].push_back({u, w});
}
vector<int> siz(n + 1, 0), max_son(n + 1, 0), vis(n + 1, 0);
function<int(int)> get_root = [&] (int u) -> int{
int res = 0;
int rt = u;
function<void(int, int)> get_siz = [&] (int u, int fa) {
siz[u] = 1;
for (auto [v, w] : g[u]) {
if (v == fa || vis[v]) continue;
get_siz(v, u);
siz[u] += siz[v];
}
};
function<void(int, int)> dfs = [&] (int u, int fa) {
max_son[u] = 0;
for (auto [v, w] : g[u]) {
if (v == fa || vis[v]) continue;
dfs(v, u);
max_son[u] = max(max_son[u], siz[v]);
}
max_son[u] = max(max_son[u], siz[rt] - siz[u]);
if (res == 0 || max_son[u] < max_son[res])
res = u;
};
get_siz(u, 0);
dfs(u, 0);
return res;
};
function<vector<int>(int, int)> get_dis = [&](int u, int add) -> vector<int>{
vector<int> res;
function<void(int, int, int)> dfs = [&] (int u, int fa, int d) {
res.push_back(d);
for (auto [v, w] : g[u]) {
if (v == fa || vis[v]) continue;
dfs(v, u, d + w);
}
};
dfs(u, 0, add);
return res;
};
function<ll(int, int, int)> solve = [&](int u, int k, int add) -> ll {
auto dis = get_dis(u, add);
sort(dis.begin(), dis.end());
vector<pair<int, int>> cnt;
for (auto x : dis) {
if (cnt.empty() || cnt.back().first != x) cnt.push_back({x, 1});
else cnt.back().second++;
}
int res = 0;
for (auto [x, y] : cnt) {
if (k % 2 == 0 && x == k / 2) res += 1ll * y * (y - 1) / 2;
}
for (int i = 0, j = (int)cnt.size() - 1; i < j; i++) {
while (j > i && cnt[i].first + cnt[j].first > k) j--;
if (j > i && cnt[i].first + cnt[j].first == k) res += 1ll * cnt[i].second * cnt[j].second;
}
return res;
};
function<ll(int, int)> dfs = [&](int u, int k) -> ll {
int root = get_root(u);
ll res = solve(root, k, 0);
vis[root] = 1;
for (auto [v, w] : g[root]) {
if (vis[v]) continue;
res -= solve(v, k, w);
}
for (auto [v, w] : g[root]) {
if (vis[v]) continue;
res += dfs(v, k);
}
return res;
};
while (m--) {
vis.assign(n + 1, 0);
int k; cin >> k;
ll ans = dfs(1, k);
// cout << ans << '\n';
cout << (ans ? "AYE" : "NAY") << '\n';
}
cout << (int)clock()/CLOCKS_PER_SEC << "s\n";
return 0;
}
PS:代码由于 function 用多了所以常数巨大