70.LCT

LCT

算法思想

Link Cut Tree / LCT 是一种数据结构，解决动态树问题，主要思想是 splay + 树链剖分

我们需要解决这样一个问题：

维护一颗树，在线询问，支持如下操作

修改两点之间路径权值
查询两点路径权值和
查询子树权值和
修改节点权值
断开并连接一些边，保证仍然是一棵树

如果没有最后一个操作，就是重链剖分的模板题

有了最后一个操作，就是动态树问题，可以使用 LCT 求解

对于树链剖分，我们每次选择子树最大的儿子作为重儿子，把树分成若干重链和若干轻链，然后使用线段树等数据结构处理

对于动态树，我们也利用类似的思想，对于每个点，连向它儿子的所有边，我们选择一条边进行剖分，被选择的边称为实边，其他的边为虚边，实边连接的儿子称为实儿子，对于一条实边连成的链，称为实链，我们把 LCT 的这种剖分方式叫做实链剖分

注意：实链剖分中的实儿子不一定是重儿子，任意一个即可

在实链剖分后，我们利用 Splay 树来维护实链

感性地说，LCT 利用若干 Splay 来维护动态的树链剖分，以期实现动态树上的区间操作。

对于每条实链，建立一棵 Splay 来维护整条链的信息

辅助树

每棵辅助树维护的是对应的一颗原树，若干辅助树维护的是对应的森林

一棵辅助树由若干棵 Splay 组成，每颗 Splay 维护原树中的一条实链，中序遍历某棵 Splay，得到的点序列，对应于原树从上到下访问这条路径得到的点的序列（也就是说，点在 Splay 中的排序权值实其在原树中的深度）

对于实边，我们建立 Splay 来维护，那么对于虚边，我们通过建立当前 Splay 的根节点到另一个点的单向路径，注意这里儿子认父亲，但父亲不认儿子

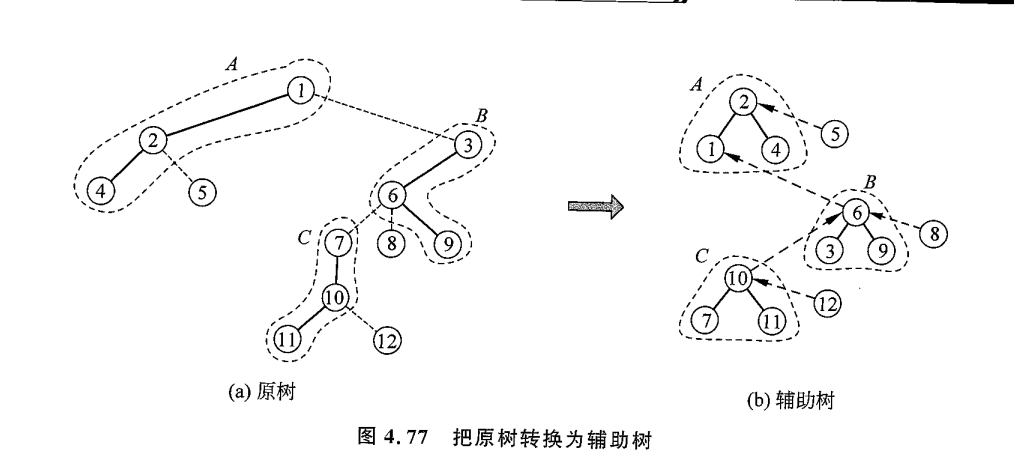
图中， $3$ -> $1$ 是一条虚边，我们找到 $3$ 所在 Splay 的根节点 $6$ ，然后连接 $6$ -> $1$

这种建边方式并不会造成信息的丢失，我们可以通过找到当前所在 Splay 深度最小的节点，也就是最 “左边” 的节点来还原原树

有了辅助树，我们可以不需要维护原树，通过辅助树能维护原树上的一些信息

辅助树可以在满足其性质前提下，利用 Splay 操作任意换根，但是对于每个 Splay 树上的 Splay 提根操作都不会影响 BST 的性质，所以对应的原树也不会改变

虚实链变换可以在辅助树上轻松完成，这就实现了动态树链剖分

算法实现

按照洛谷模板题【模板】动态树（LCT）来写示例

首先需要声明一些变量

struct node{
    int fa,ch[2],sum,val,lay;
}t[maxn];

前置函数

bool is_root(int x){ // 判断x是否为根
    int f = t[x].fa;
    return t[f].ch[0] != x && t[f].ch[1] != x;
}

void push_up(int x){
    t[x].sum = t[x].val ^ t[t[x].ch[0]].sum ^ t[t[x].ch[1]].sum;
}

void reverse(int x){
    if(!x) return ;
    swap(t[x].ch[0],t[x].ch[1]);
    t[x].lay ^= 1;
}

void push_down(int x){
    if(t[x].lay){
        reverse(t[x].ch[0]);
        reverse(t[x].ch[1]);
        t[x].lay = 0;
    }
}

void push(int x){ // 递归标记下传
    if(!is_root(x)) push(t[x].fa);
    push_down(x);
}

void rotate(int x){ //旋转
    int f = t[x].fa;
    int g = t[f].fa;
    int k = t[f].ch[1] == x;
    if(!is_root(f)) //如果 f 不是根
        t[g].ch[t[g].ch[1] == f] = x;
    t[x].fa = g;
    
    t[f].ch[k] = t[x].ch[k^1];
    if(t[x].ch[k^1]) t[t[x].ch[k^1]].fa = f;

    t[x].ch[k^1] = f; t[f].fa = x;
    push_up(f); push_up(x);
}

void splay(int x){  //题根，将x旋转到根
    int f,g;
    push(x);
    while(!is_root(x)){
        f = t[x].fa, g = t[f].fa;
        if(!is_root(f))
            (t[f].ch[0] == x) ^ (t[g].ch[0] == f) ? rotate(x) : rotate(f);
        rotate(x);
    }
    push_up(x);
}

access

其中 access 是最核心的功能，用于将原树上的根到 $x$ 的路径变成实链

void access(int x){  // 在 原树 上建一条实链，起点是根，终点是x
    for(int p = 0; x; p = x, x = t[x].fa){
        splay(x);
        t[x].ch[1] = p;  // 将x的右儿子设置为 p
        push_up(x);
    }
}

代码短小而精悍

access 的操作具体的做了两件事情

将根到 $x$ 的路径上的点放在同一棵 Splay 中
让 $x$ 的实儿子不在 Splay 中

一次 access 操作做了如下操作

将当前指向节点旋转到根
把儿子换成之前的节点
更新当前信息
指针向上，跳到下一棵 Splay 树上面

为什么这样就能让根到 $x$ 的所有边变成实边呢？

我们一路旋转向上，所经过的每个点都被转到根，并且都与上一个在根的点用实边相连。

然后，每个点都抛弃了它原先的右儿子，而将原本以虚边连接的路径上的上一个点设置为右儿子，这样子就能保证之前的那个点 $p$ 和 $x$ 在同一条实链上面了

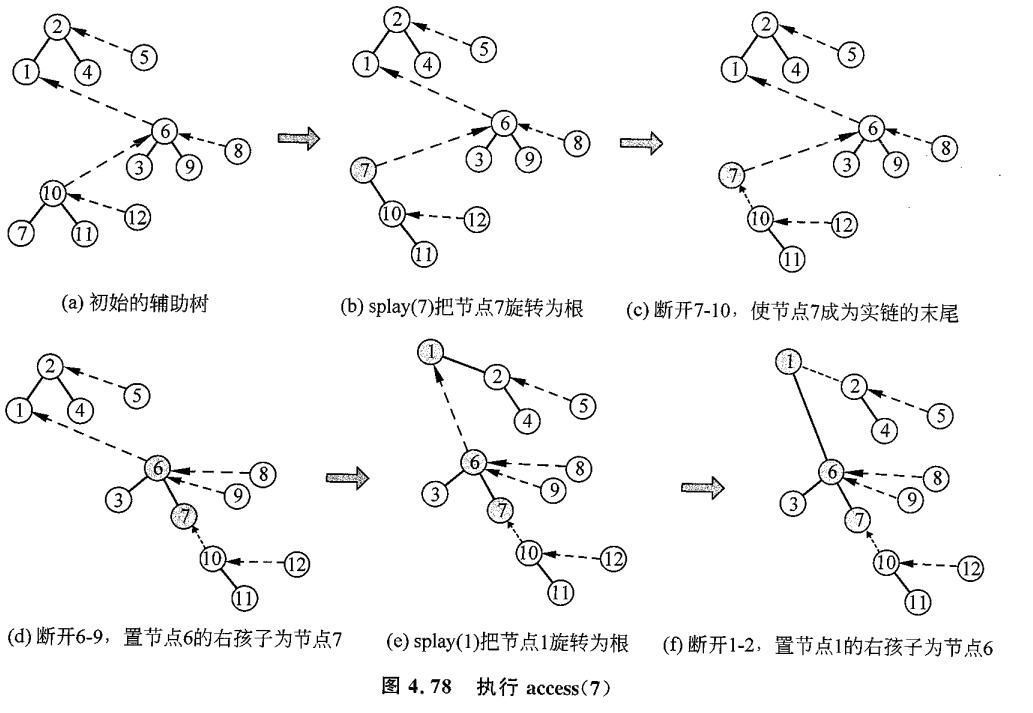
这张图有效体现了 access(7) 的全过程

再想想为什么会成功？

一棵 Splay 的根到其父节点的边，一定对应原树上的一条虚边，每次我们先 splay(x) 用于把 $x$ 节点调整到这棵 Splay 的根节点，那么 $t [x] . f a$ 必定连接的是一条虚边，而这条虚虚边在原树上肯定也对应一条虚边，然后把这条实变变成虚变的过程中，丢弃了原来的实儿子
为什么连接右儿子，因为根据辅助树的性质，其中序遍历对应原树上的遍历，原树的父节点的深度小于子节点，所以 Splay 树上就是右儿子

make_root

这个函数的重要性不低于 access

我们在维护路径信息的时候，会出现深度无法严格递增的情况，根据辅助树的性质，这种路径实无法出现在一棵 Splay 中的

此时我们需要用到 make_root 函数，把 $x$ 设为原树的根

先建立 $x$ 到根节点的实链，然后把 $x$ 设为 Splay 的根节点，因为根据辅助树的性质， $x$ 在所有数的右边，也就是说，所有数都在 $x$ 的左儿子上

那么怎么把 $x$ 提到原树的根呢，只需要翻转 Splay，就是把所有的左儿子和右儿子对调

具体实现是，不需要马上翻转每个节点，类似于线段树的方法做一个懒标记，遍历到的时候下传即可

void reverse(int x){
    if(!x) return ;
    swap(t[x].ch[0],t[x].ch[1]);
    t[x].lay ^= 1;
}

void make_root(int x){ // 将 x 在原树上旋转到根的位置
    access(x);  // 建立一条实链
    splay(x);  // 把 x 旋转到当前 splay 树的根
    reverse(x); // 反转
}

push_down

一般来说，懒标记有两种写法

我所常用的写法是：当前节点有翻转标记，表示当前节点已经翻转了，但是子节点没有翻转

void push_down(int x){
    if(t[x].lay){
        reverse(t[x].ch[0]);
        reverse(t[x].ch[1]);
        t[x].lay = 0;
    }
}

split

void split(int x,int y){ // 把原树上以 x 为起点，以 y 为终点的路径，生成一条实链
    make_root(x); // 将 x 旋转到根
    access(y); // 建立一条实链
    splay(y); // 把 y 旋转到当前 splay 树的根，方便之后的操作
}

link

void link(int x,int y){ // 在原树上连接 x 和 y
    make_root(x); // 将 x 旋转到根
    t[x].fa = y; // 将 x 的父亲设置为 y
}

cut

void cut(int x,int y){  // 切断 x,y 之间连的边
    split(x,y);
    if(t[y].ch[0] != x || t[x].ch[1]) return ; // 如果 x,y 不直接相连，直接返回
    t[y].ch[0] = t[x].fa = 0; // 切断 x,y 之间的边
    push_up(y); push_up(x);
}

注意 $x, y$ 在同一棵原树上，但是有可能不相连，对应到 Splay 上面就不是连续的了，所以 t[y].ch[0] != x || t[x].ch[1] 就能判断

find_root

int find_root(int x){ //查找 x 在原树上的根
    access(x); splay(x);
    while(t[x].ch[0]) x = t[x].ch[0];
    return x;
}

完整代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e5 + 5;

int read(){
    int x = 0, f = 1; char ch = getchar();
    while(!isdigit(ch)){if(ch == '-') f = -1; ch = getchar();}
    while(isdigit(ch)){x = x * 10 + ch - '0'; ch = getchar();}
    return x * f;
}

struct node{
    int fa,ch[2],sum,val,lay;
}t[maxn];

bool is_root(int x){ // 判断x是否为根
    int f = t[x].fa;
    return t[f].ch[0] != x && t[f].ch[1] != x;
}

void push_up(int x){
    t[x].sum = t[x].val ^ t[t[x].ch[0]].sum ^ t[t[x].ch[1]].sum;
}

void reverse(int x){
    if(!x) return ;
    swap(t[x].ch[0],t[x].ch[1]);
    t[x].lay ^= 1;
}

void push_down(int x){
    if(t[x].lay){
        reverse(t[x].ch[0]);
        reverse(t[x].ch[1]);
        t[x].lay = 0;
    }
}

void push(int x){ // 递归标记下传
    if(!is_root(x)) push(t[x].fa);
    push_down(x);
}

void rotate(int x){ //旋转
    int f = t[x].fa;
    int g = t[f].fa;
    int k = t[f].ch[1] == x;
    if(!is_root(f)) //如果 f 不是根
        t[g].ch[t[g].ch[1] == f] = x;
    t[x].fa = g;
    
    t[f].ch[k] = t[x].ch[k^1];
    if(t[x].ch[k^1]) t[t[x].ch[k^1]].fa = f;

    t[x].ch[k^1] = f; t[f].fa = x;
    push_up(f); push_up(x);
}

void splay(int x){  //题根，将x旋转到根
    int f,g;
    push(x);
    while(!is_root(x)){
        f = t[x].fa, g = t[f].fa;
        if(!is_root(f))
            (t[f].ch[0] == x) ^ (t[g].ch[0] == f) ? rotate(x) : rotate(f);
        rotate(x);
    }
    push_up(x);
}

void access(int x){  // 在 原树 上建一条实链，起点是根，终点是x
    for(int p = 0; x; p = x, x = t[x].fa){
        splay(x);
        t[x].ch[1] = p;  // 将x的右儿子设置为 p
        push_up(x);
    }
}

void make_root(int x){ // 将 x 在原树上旋转到根的位置
    access(x);  // 建立一条实链
    splay(x);  // 把 x 旋转到当前 splay 树的根
    reverse(x); // 反转
}

void split(int x,int y){ // 把原树上以 x 为起点，以 y 为终点的路径，生成一条实链
    make_root(x); // 将 x 旋转到根
    access(y); // 建立一条实链
    splay(y); // 把 y 旋转到当前 splay 树的根，方便之后的操作
}

void link(int x,int y){ // 在原树上连接 x 和 y
    make_root(x); // 将 x 旋转到根
    t[x].fa = y; // 将 x 的父亲设置为 y
}

void cut(int x,int y){  // 切断 x,y 之间连的边
    split(x,y);
    if(t[y].ch[0] != x || t[x].ch[1]) return ; // 如果 x,y 不直接相连，直接返回
    t[y].ch[0] = t[x].fa = 0; // 切断 x,y 之间的边
    push_up(y); push_up(x);
}

int find_root(int x){ //查找 x 在原树上的根
    access(x); splay(x);
    while(t[x].ch[0]) x = t[x].ch[0];
    return x;
}

int main(){
    // freopen("P3690.in","r",stdin);
    int n = read(), m = read();
    for(int i=1;i<=n;i++) {
        t[i].val = read();
        t[i].sum = t[i].val;
        t[i].ch[0] = t[i].ch[1] = t[i].fa = 0;
    }

    while(m--){
        int op = read(), a = read(), b = read();
        if(op == 0) {split(a,b); printf("%d\n",t[b].sum);}
        if(op == 1) {if(find_root(a) != find_root(b)) link(a,b);}
        if(op == 2) {if(find_root(a) == find_root(b)) cut(a,b);}
        if(op == 3) {splay(a); t[a].val = b; push_up(a);}
    }
    return 0;
}

基本应用

判断连通性

判断两节点 $a, b$ 是否连通只需判断 $f i n d_r o o t (a)$ 是否等于 $f i n d_r o o t (b)$

求两点之间的距离

先执行 $s p l i t (x, y)$ 然后累加这颗 Splay 树的边权，一样使用 Lazy 标记提高效率

求 LCA

用 LCT 求 LCA，只需要利用 access() 函数

利用 $a c c e s s (x)$ 建立一条从根到 $x$ 的实链，显然 $L C A (x, y)$ 在这条链上

然后对 $y$ 执行 $a c c e s s (y)$ 操作，沿着原树向根走，肯定会遇到 $v$ 在之前 $a c c e s s (x)$ 已经建好的实链上，这个点 $v$ 就是 $L C A (x, y)$

这个过程在辅助树上看其实更简单，如果走到了根所在 Splay 树，就找到了 $v$ ，那么怎么判断这颗 Splay 是否包含原树根节点，只需要 $s p l a y (v)$ ，然后看 $t [x] . f a$ 是否为零即可