60.差分约束
差分约束
差分约束系统 是一种特殊的
我们要解决的问题是:求一组解
很多题目会给出(或隐性地给出)一系列的不等关系,我们可以尝试把它们转化为差分约束系统来解决。
我们设
观察这个不等式与最短路问题中的三角形不等式
这样建出的有向图,它的每个顶点都对应差分约束系统中的一个未知量,源点到每个顶点的最短路对应这些未知量的值,而每条边对应一个约束条件
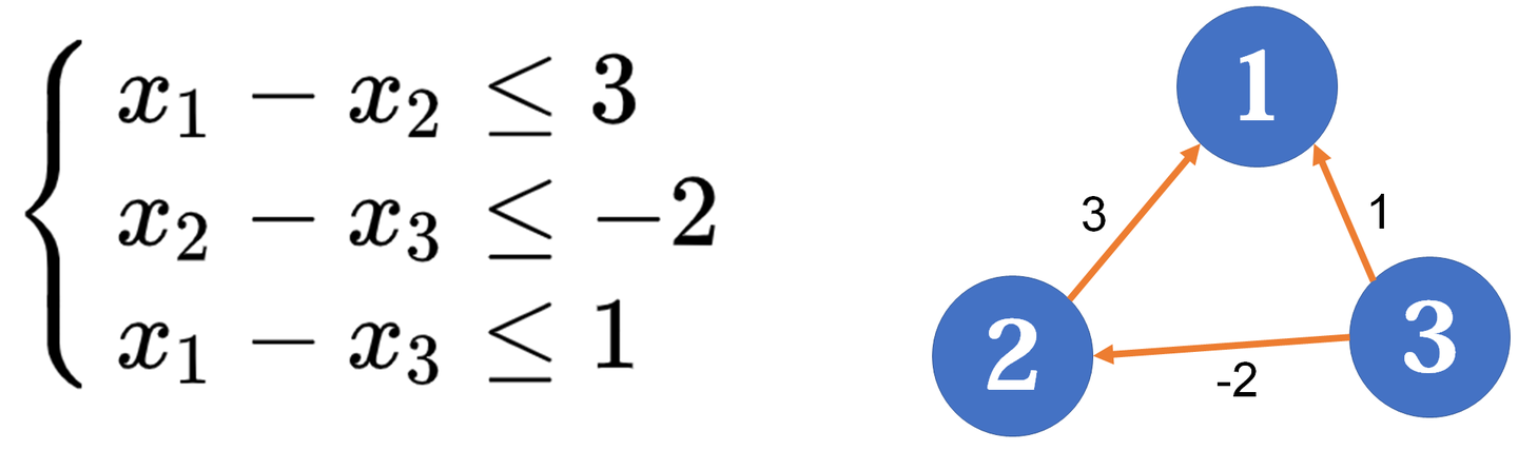
那么问题来了,既然是最短路,源点在哪里呢?
实际上取哪个点为源点是无关紧要的,但是,有时候我们得到的图不是连通的,这样求出来的结果很容易出现INF。为了避免这种情形,我们习惯人为地增加一个超级源点
例如我们现在人为地新增一个
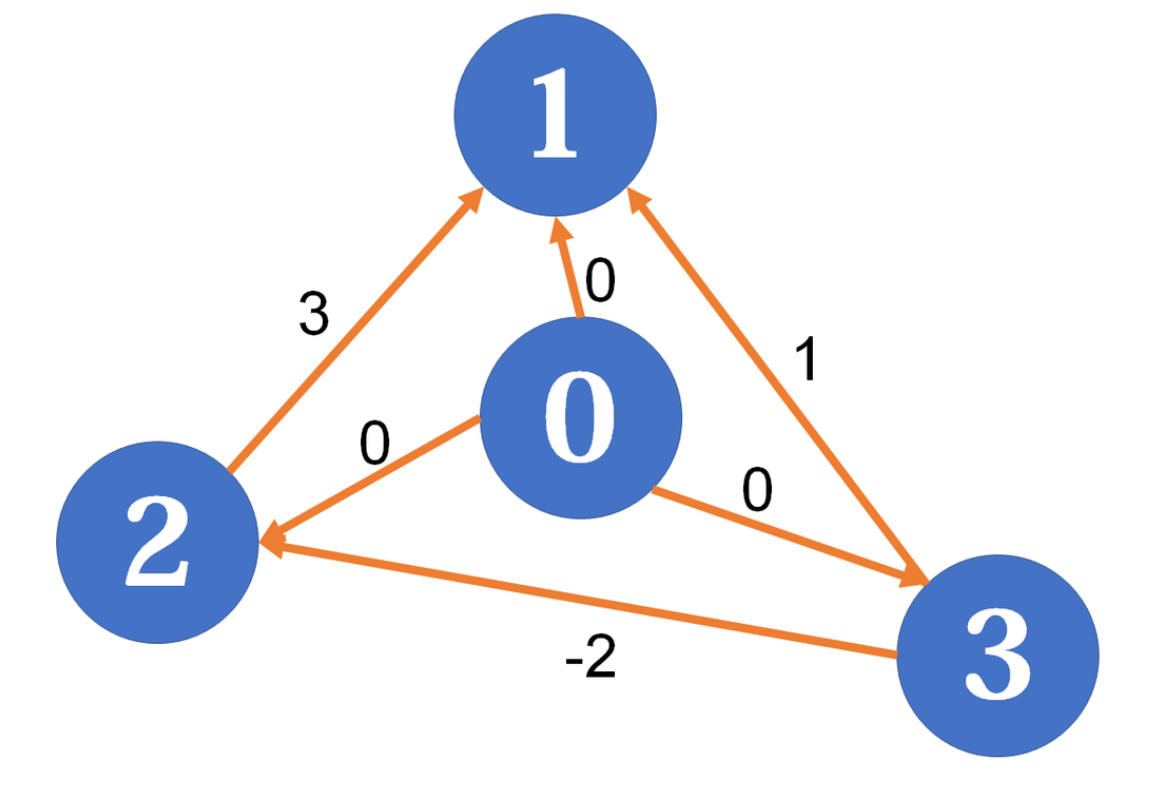
现在我们以
由于
因为这样求出来的只是一组解,显然,如果
那么如果题目要求
那么如何求满足
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int INF = 0x3f3f3f3f;
int main() {
int n, m; cin >> n >> m;
vector<vector<pii>> g(n + 1);
for (int i = 1; i <= m; i++) {
int x, y, c; cin >> x >> y >> c;
g[y].push_back({x, c});
}
for (int i = 1; i <= n; i++) g[0].push_back({i, 0});
vector<int> dis(n + 1, INF), vis(n + 1, 0), cnt(n + 1, 0);
auto spfa = [&]() -> bool {
queue<int> q;
q.push(0); vis[0] = 1; dis[0] = 0; cnt[0] = 1;
while (!q.empty()) {
int u = q.front(); q.pop(); vis[u] = 0;
for (auto [v, w] : g[u]) {
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
if (!vis[v]) {
q.push(v); vis[v] = 1;
if (++cnt[v] > n) return false;
}
}
}
}
return true;
};
if (spfa()) {
for (int i = 1; i <= n; i++)
cout << dis[i] << ' ';
}
else
printf ("NO\n");
return 0;
}