20.DP优化
DP 优化
单调队列优化 DP
单调队列在 DP 中优化的基本应用,是对这样一类 DP 状态转移方程进行优化
方程的特点是其中关于
如果单纯的枚举
我们假设
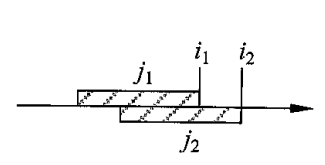
在
考虑维护
那么如何取得答案?如果这是一个单调递增的队列,那就取头,如果头部的节点不合法,在
四边形不等式优化 DP
一些常用的区间 DP 问题的状态转移方程为:
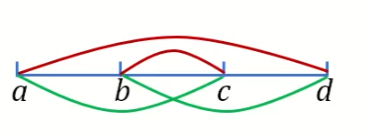
- 四边形不等式:设
有, ,包含和 交叉和 - 单调性:设
满足:
DP 转移的最后一层
for (int len = 1; len <= n; len ++)
for (int i = 1; i + len - 1 <= n; i ++){
int j = i + len - 1;
for (int k = p[i][j-1]; k <= p[i + 1][j]; k ++){
if(dp[i][j] > dp[i][k] + dp[k + 1][j] + w[i][j]){
dp[i][j] = dp[i][k] + dp[k + 1][j] + w[i][j];
p[i][j] = k;
}
}
}
其中