12.三维计算几何基础

三维计算几何基础

定义

struct Point3{
    double x,y,z;
    Point3(double x=0,double y=0,double z=0):x(x),y(y),z(z){}
};
typedef Point3 Vector3;

基本运算

Vector3 operator +(Vector3 A,Vector3 B){return Vector3(A.x+B.x,A.y+B.y,A.z+B.z);}
Vector3 operator -(Point3 A,Point3 B){return Vector3(A.x-B.x,A.y-B.y,A.z-B.z);}
Vector3 operator *(Vector3 A,double p){return Vector3(A.x*p,A.y*p,A.z*p);}
Vector3 operator /(Vector3 A,double p){return Vector3(A.x/p,A.y/p,A.z/p);}

直线的表示，可以用参数方程（点和向量）来表示，射线和线段可以看成”参数由取值范围限制的“的直线

平面的表示，用点法式 $(p_{0}, n)$ ，其中 $p_{0}$ 是平面上的一个点，向量 $n$ 是平面的法向量。每个平面把空间分成了两个部分，我们用点法式表示其中一个半空间，是法向量所背离的哪一个。 $n$ 垂直于平面上的所有直线。平面上任意点 $p$ 满足 $D o t (n, p - p_{0}) = 0$ 。设 $p$ 的坐标为 $(x, y, z)$ ， $p_{0}$ 的坐标为 $(x_{0}, y_{0}, z_{0})$ ，向量 $n$ 的坐标表示为 $(A, B, C)$ 上述等式等价于

A (x - x_{0}) + B (y - y_{0}) + C (z - z_{0}) = 0

整理得： $A x + B y + C z - (A x_{0} + B y_{0} + C z_{0}) = 0$ 如果令 $- (A x_{0} + B y_{0} + C z_{0})$ ，就得到了平面的一般式

A x + B y + C z + D = 0

当 $A x + B y + C z + D > 0$ 上述点积大于 $0$ ，即点 $(x, y, z)$ 在半平面空间 $(p_{0}, n)$ 外。换句话说 $A x + B y + C z + D > 0$ 表示的是以一个半空间

点积

double dot(Vector3 A, Vector3 B) { return A.x * B.x + A.y * B.y + A.z * B.z; }

长度

double length(Vector3 A) { return sqrt(dot(A, A)); }

向量夹角

double angle(Vector3 A, Vector3 B) { return acos(dot(A, B) / length(A) / length(B)); }

叉积

三维叉积的结果是一个向量

v_{1} \times v_{2} = [\begin{matrix} y_{1} z_{2} - y_{2} z_{1} \\ z_{1} x_{2} - z_{2} x_{1} \\ x_{1} y_{2} - x_{2} y_{1} \end{matrix}]

叉积同时垂直于 $v_{1}$ 和 $v_{2}$ ，方向遵循右手定则。当且仅当 $v_{1}$ 和 $v_{2}$ 平行时，叉积为 $0$

Vector3 cross(Vector3 A, Vector3 B) {
    return Vector3(A.y * B.z - A.z * B.y, A.z * B.x - A.x * B.z, A.x * B.y - A.y * B.x);
}

通过向量叉积，可以进行一些拓展的基础问题。

过不共线的三点的平面，法向量为 $Cross (p_{2} - p_{0}, p_{1} - p_{0})$ ，任取一个点即可得到平面的点法式。

三角形的有向面积的两倍

double area2(Point3 A, Point3 B, Point3 C) { return length(cross(B - A, C - A)); }

点、线、面

点到直线的距离

double distance_to_line(Point3 p, Point3 p0, Vector3 v) {
    return length(cross(p - p0, v)) / length(v);
}

点在直线上的投影

Point3 line_projection(Point3 p, Point3 p0, Vector3 v) {
    return p0 + v * dot(p - p0, v) / dot(v, v);
}

点到平面的距离

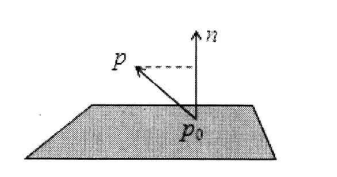
把 $p - p_{0}$ 投影到向量 $n$ 上可得： $p$ 到平面的有向距离为 $D o t (p - p_{0}, n) / L e n g t h (n)$ 。

double distance_to_plane(Point3 p, Point3 p0, Vector3 n) {
    return fabs(dot(p - p0, n) / length(n));
}  //点 p 到平面 p0-n 的距离，如果不取绝对值，得到的是有向距离

点在平面上的投影点

设 $p$ 在平面 $(p_{0}, n)$ 上的投影为 $p^{'}$ 则 $p^{'} - p$ 平行于 $n$ ，且 $p^{'} - p = d n$ 其中 $d$ 为 $p$ 到平面的的有向距离

Point3 plane_projection(Point3 p, Point3 p0, Vector3 n) {
    return p - n * dot(p - p0, n) / length(n);
}

直线和直线的交点

Point3 line_intersection(Point3 p, Vector3 v, Point3 q, Vector3 w) {
    Vector3 u = p - q;
    double t = length(cross(w, u)) / length(cross(v, w));
    return p + v * t;
}

直线和平面的交点

设平面方程为 $Dot (n, p - p_{0}) = 0$ ，过点 $p_{1}$ 和 $p_{2}$ 的直线的参数方程为 $p = p_{1} + t (p_{2} - p_{1})$ ，则与平面方程联立解得

t = Dot (n, p_{0} - p_{1}) / Dot (n, p_{2} - p_{1})

如果分母为 $0$ 则直线和平面平行，或者直线在平面上

如果平面用一般式 $A x + B y + C z + D = 0$ ，则联立出来的表达式为

t = \frac{A x_{1} + B y_{1} + C z_{1} + D}{A (x_{1} - x_{2}) + B (y_{1} - y_{2}) + C (z_{1} - z_{2})}

Point3 line_plane_intersection(Point3 p, Vector3 v, Point3 p0, Vector3 n) {
    Vector3 u = p - p0;
    double t = dot(n, u) / dot(n, v);
    return p - v * t;
}

体

四面体的体积

已知 $4$ 个顶点为 $A, B, C, D$

V = \frac{1}{3} S \cdot h = \frac{1}{6} (\vec{A B} \times \vec{A C}) \cdot h = \frac{1}{6} (\vec{A B} \times \vec{A C}) \cdot \vec{A D}

double volume6(Point3 A, Point3 B, Point3 C, Point3 D) {
    return dot(D - A, cross(B - A, C - A));
}