30.多项式与生成函数

多项式与生成函数

生成函数

母函数（又翻为生成函数），是求解递推关系巧妙的数学方法，他通过代数手段解决组合计数问题

先思考一个简单的问题：从数字 $1, 2, 3, 4$ 中取出一个或多个相加（每个数字最多只能用一次）能组合成几个数？每个数有几种组合？

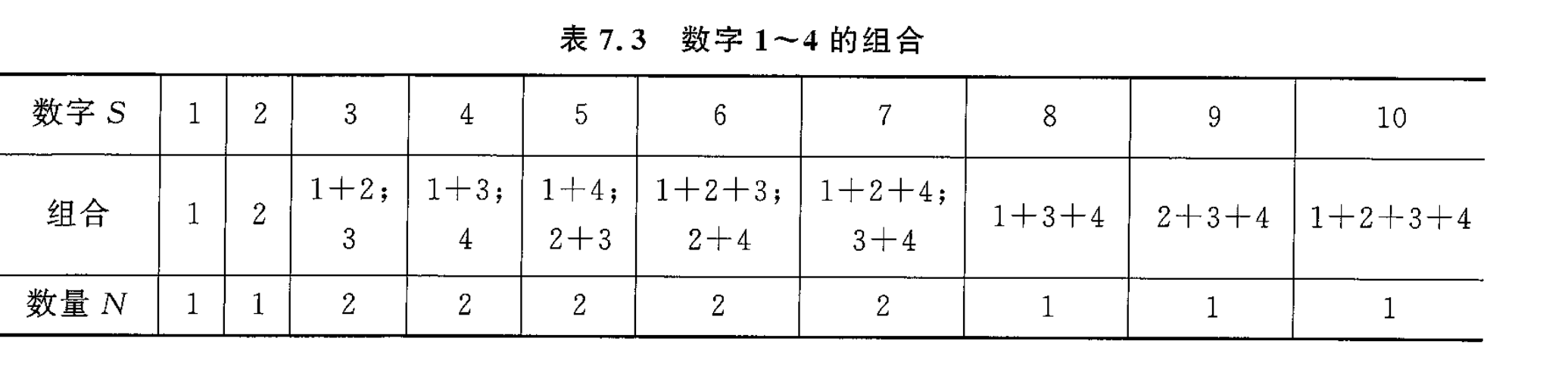
我们构造一个多项式，把他展开

(1 + x) (1 + x^{2}) (1 + x^{3}) (1 + x^{4}) = 1 + x + x^{2} + 2 x^{3} + 2 x^{4} + 2 x^{5} + 2 x^{6} + 2 x^{7} + x^{8} + x^{9} + x^{10}

惊人的发现，每个数的组合数量和系数一样

母函数的作用就是这样：把组合问题的加法与幂级数的乘幂对应起来

普通母函数的定义：对于序列 $h_{0}, h_{1}, h_{2}, \dots,$ 构造函数 $g (x) = h_{0} + h_{1} x + h_{2} x^{2} \dots$ ，称 $g (x)$ 为序列 $h_{0}, h_{1}, h_{2}, \dots$ 的母函数

母函数的实质是无限可微分函数的泰勒计数，有：

\frac{1}{1 - x} = 1 + x + x^{2} + \dots

\frac{1}{1 - x^{2}} = 1 + x^{2} + x^{4} + \dots

利用母函数的泰勒计数表达，有时可以简单的演算组合计数问题

在袋子中装 $n$ 个水果，要求苹果是偶数个，香蕉数是 $5$ 的倍数，句子最多 $4$ 个，梨有 $0$ 个或 $1$ 个，给出 $n$ ，共有多少种情况？

写出生成函数：

\begin{aligned} g (x) & = (1 + x^{2} + x^{4} + \dots) (1 + x^{5} + x^{10} + \dots) (1 + x + x^{2} + x^{3} + x^{4}) (1 + x) \\ = \frac{1}{1 - x^{2}} \frac{1}{1 - x^{5}} \frac{1 - x^{5}}{1 - x} (1 + x) \\ = \frac{1}{(1 - x)^{2}} \\ = \sum_{k = 0}^{\infty} (n + 1) x^{n} \end{aligned}

最后一步根据牛顿二项式定理得到

幂级数

多项式： $A (x) = \sum_{i = 0}^{n} a_{i} x^{i}$
形式幂级数： $A (x) = \sum_{i \geq 0} a_{i} x^{i}$

形式幂级数之间可以有一些运算：

设 $A (x) = \sum_{i \geq 0} a_{i} x^{i}, B (x) = \sum_{i \geq 0} b_{i} x^{i}$

加法： $A (x) + B (x) = \sum_{i \geq 0} (a_{i} + b_{i}) x^{i}$
乘法： $A (x) B (x) = \sum_{k \geq 0} (\sum_{i + j = k} a_{i} b_{j}) x^{i}$

我们发现，乘法和多项式乘法有共同之处

形式幂级数

记形式幂级数（或多项式） $A (x)$ 的 $x^{n}$ 项的系数为 $[x^{n}] A (x)$

形式幂级数的本质是序列，幂级数的本质是极限

形式幂级数的逆元

形式幂级数 $A (x)$ 的逆元： $A (x) B (x) = 1$
逆元存在的条件： $[x^{0}] A (x) \neq 0$

常见的逆：

$A (x) = 1 + x + x^{2} + \dots$ 的逆元为 $B (x) = 1 - x$
$A (x) = 1 + a x + a^{x} x^{2} + \dots$ 的逆元为 $B (x) = 1 - a x$
$A (x) = C_{k - 1}^{0} + C_{k}^{1} x + C_{k + 1}^{2} x^{2} + C_{k + 1}^{3} x^{3} + \dots$ 的逆元为 $B (x) = (1 - x)^{k}$ ，即 $A (x) = \frac{1}{(1 - x)^{k}} = \sum_{i \geq 0} C_{i + k - 1}^{i} x^{i}$

形式幂级数的求导

假设 $f (x) = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{n} x^{n} + \dots$

定义 $f (x)$ 的导数为 $a_{1} + 2 a_{2} x + \dots + (n + 1) a_{n + 1} x^{n} + \dots$ 记作 $f^{'} (x)$ 或 $\frac{d f (x)}{d x}$

形式幂级数的积分

假设 $f (x) = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{n} x^{n} + \dots$

定义 $f (x)$ 的积分为 $a_{0} x + \frac{a_{1}}{2} x^{2} + \dots + \frac{a_{n - 1}}{n} x^{n} + \dots$ 记作 $\int f (x) d x$

形式幂级数的复合

假设 $f (x) = a_{1} x + \dots + a_{n} x^{n} + \dots$ ， $g (x) = b_{0} + b_{1} x + \dots + b_{n} x^{n} + \dots$

$g$ 复合 $f$ 定义为 $c_{0} + c_{1} x + \dots + c_{n} x^{n} + \dots$ ，满足 $c_{0} = b_{0}, c_{n} = \sum_{k = 1}^{n} b_{k} \sum_{i_{1} + i_{2} + \dots + i_{k} = n} a_{i_{1}} a_{i_{2}} \dots a_{i_{k}}$ ，记为 $g (f (x))$

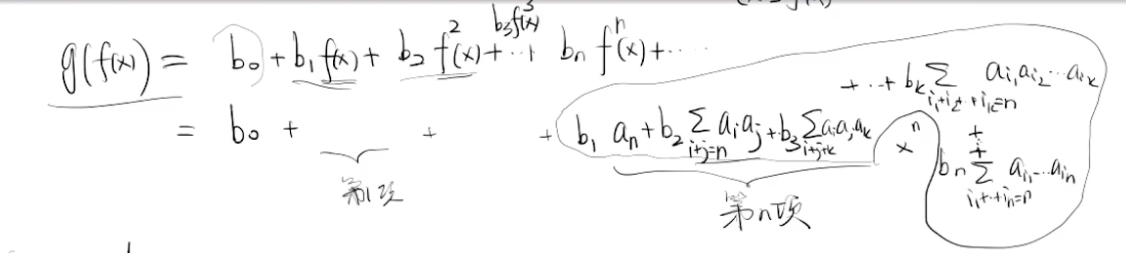
形式幂级数的其他运算

$\exp (x) = \sum_{n \geq 0} \frac{1}{n!} x^{n}$
$\ln (1 + x) = \sum_{n \geq 1} \frac{(- 1)^{n + 1}}{n} x^{n}$
设形式幂级数 $f (x)$ 满足 $[x^{0}] f (x) = 0$ 由此可以定义 $\exp (f (x))$ 和 $\ln (f (x) + 1)$ ，或者可以定义 $[x^{0}] f (x) = 1$ 则可以计算 $\ln (f (x))$

常生成函数

一个数列 ${a_{n}}$ 对应的常数生成函数为 $A (x) = \sum_{n \geq 0} a_{n} x^{n}$

例: 有两种物品，其中取 $i$ 个第 $1$ 种物品的方案数为 $a_{i}$ ，取 $j$ 个第二种物体的方案数为 $b_{j}$ ，求取 $k$ 个物体的方案数

设 $A (x) = \sum_{i \geq 0} a_{i} x^{i}, B (x) = \sum_{j \geq 0} b_{j} x^{j}$

答案为 $C (x) = A (x) B (x)$

递推关系

斐波那契数列满足 $a_{0} = 0, a_{1} = 1, a_{n} = a_{n - 1} + a_{n - 2} (n \geq 2)$ ，求其生成函数

设 $A (x) = \sum_{n \geq 0} a_{n} x^{n}$

\begin{aligned} A (x) & = a_{0} + a_{1} x + a_{2} x^{2} + \dots \\ = 0 + x + (a_{0} + a_{1}) x^{2} + (a_{1} + a_{2}) x^{3} + \dots + (a_{n - 2} + a_{n - 1}) x^{n} + \dots \\ = x + (a_{1} x^{2} + a_{2} x^{3} + a_{3} x^{4} + \dots) + (a_{1} x^{3} + a_{2} x^{4} + \dots) \\ = x + x A (x) + x^{2} A (x) \end{aligned}

解得 $A (x) = \frac{x}{1 - x - x^{2}}$

我们可以通过这个常生成函数来求数列的第 $n$ 项

把分数拆开，有：

A (x) = \frac{x}{1 - x - x^{2}} = x (\frac{c}{1 - a x} + \frac{d}{1 - b x})

那么： $[x^{n}] A (x) = c \cdot a^{n} + d \cdot b^{n}$

上面的 $a, b, c, d$ 可以使用待定系数法求解

指数生成函数

一个数列 ${a_{n}}$ 对应的指数生成函数为 $A (x) = \sum_{n \geq 0} a_{n} \frac{x^{n}}{n!}$

有两个物体，其中取 $i$ 个第 $1$ 种物品的方案数为 $a_{i}$ ，取 $j$ 个第二种物体的方案数为 $b_{j}$ ，求取 $k$ 个物体并排成一列的方案数

设 $A (x) = \sum_{i \geq 0} a_{i} \frac{x^{i}}{i!}, B (x) = \sum_{j \geq 0} b_{j} \frac{x^{j}}{j!}$

\begin{aligned} c_{k} & = \sum_{i = 0}^{k} (\binom{k}{i}) a_{i} b_{k - i} \\ = \sum_{i = 0}^{k} \frac{k!}{i! (k - i)!} a_{i} b_{k - i} \\ \frac{c_{k}}{k!} & = \sum_{i = 0}^{k} \frac{a_{i}}{i!} \frac{b_{k - i}}{(k - i)!} \\ C (x) & = A (x) B (x) \end{aligned}

所以答案为 $C (x) = A (x) B (x)$

$\exp (x) = 1 + x + \frac{x^{2}}{2!} + \dots = \sum_{n \geq 0} \frac{x^{n}}{n!}$
$\exp (n x) = 1 + n x + \frac{n^{2} x^{2}}{2!} + \dots = \sum_{n \geq 0} \frac{n^{n} x^{n}}{n!}$

使用 $\exp$ 函数就可以实现生成函数之间的运算了，比如 $\exp (a) \exp (b) = \exp (a + b)$

FFT

朴素多项式乘法，求逆，开根号等的复杂度为 $O (n^{2})$

FFT / NTT 可以 $O (n \log n)$ 内实现两个 $n$ 次多项式的乘积

多项式的表示形式

假设 $f (x)$ 是一个 $n$ 次多项式，则 $f (x)$ 的系数表示为 $f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{0}$

则 $f (x)$ 的点值表示为 $(x_{0}, f (x_{0})), (x_{1}, f (x_{1})), \dots, (x_{n}, f (x_{n}))$

那么也就是说 $n + 1$ 个点值可以表示一个 $n$ 次多项式

在点值表示下 $n$ 次多项式的乘法复杂度为 $O (n)$

复数与单位根

复数的指数形式

$a + b_{i} = r e^{i θ}$ ，其中 $t = \sqrt{a^{2} + b^{2}}$ ， $t a n (θ) = \frac{b}{a}$

单位根

$x^{n} = 1$ 在复数域上的根称为 $n$ 次单位根。 $n$ 次单位根有 $n$ 个，形式为 $w_{n}^{k} = e^{i \frac{2 k π}{n}}$

单位根的性质：

$w_{n}^{k} = w_{2 n}^{2 k}$
$w_{2 n}^{k + n} = - w_{2 n}^{k}$

快速傅里叶变换

DFT(离散傅里叶变换)

将多项式 $A (x) = a_{0} + a_{1} x + \dots + a_{n - 1} x^{n - 1}$ 转化为其点值形式
$(w_{n}^{k}, A (w_{n}^{k})), (k = 0, 1, \dots, n - 1)$

这里如何求这个 $A (w_{n}^{k}) = d_{k}$

这里有傅里叶变换的公式：

d_{k} = \sum_{i = 0}^{n - 1} a_{i} \times w_{n}^{i k}

由于这个式子是一个线性的，所以我们能写成矩阵的形式

(\begin{matrix} d_{0} \\ d_{1} \\ d_{2} \\ ⋮ \\ d_{n - 1} \end{matrix}) = (\begin{matrix} w_{n}^{0 \times 0} & w_{n}^{0 \times 1} & w_{n}^{0 \times 2} & \dots & w_{n}^{0 \times (n - 1)} \\ w_{n}^{1 \times 0} & w_{n}^{1 \times 1} & w_{n}^{1 \times 2} & \dots & w_{n}^{1 \times (n - 1)} \\ w_{n}^{2 \times 0} & w_{n}^{2 \times 1} & w_{n}^{2 \times 2} & \dots & w_{n}^{2 \times (n - 1)} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ w_{n}^{(n - 1) \times 0} & w_{n}^{(n - 1) \times 1} & w_{n}^{(n - 1) \times 2} & \dots & w_{n}^{(n - 1) \times (n - 1)} \end{matrix}) (\begin{matrix} a_{0} \\ a_{1} \\ a_{2} \\ ⋮ \\ a_{n - 1} \end{matrix})

但是我们暴力求 ${d}$ 也是 $O (n^{2})$ 的，现在考虑一种分治做法

我们有： $A (x) = a_{0} + a_{1} x + \dots + a_{n - 1} x^{n - 1}$

把 $A (x)$ 拆成奇数项和偶数项： $A (x) = (a_{0} + a_{2} x^{2} + \dots + a_{n - 2} x^{n - 2}) + (a_{1} x + a_{3} x^{3} + a_{5} x^{5} + \dots + a_{n - 1} x^{n - 1})$

设

\begin{array}{r} B (x) = a_{0} + a_{2} x + \dots + a_{n - 2} x^{n / 2 - 1} \\ C (x) = a_{1} + a_{3} x + \dots + a_{n - 1} x^{n / 2 - 1} \end{array}

则 $A (x) = B (x^{2}) + x C (x^{2})$

当 $0 \leq k < n / 2$ 时

\begin{aligned} A (w_{n}^{k}) & = B (w_{n}^{2 k}) + w_{n}^{k} C (w_{n}^{2 k}) \\ = B (w_{n / 2}^{k}) + w_{n}^{k} C (w_{n / 2}^{k}) \end{aligned}

当 $n / 2 < k$ 时

不妨把 $k$ 减小 $n / 2$ 继续把 $k$ 控制在 $0 \leq k < n / 2$ 的范围内

\begin{aligned} A (w_{n}^{k + n / 2}) & = B (w_{n}^{2 k + n}) + w_{n}^{k + n / 2} C (w_{n}^{2 k + n}) \\ = B (w_{n}^{2 k}) + w_{n}^{k + n / 2} C (w_{n}^{2 k}) \\ = B (w_{n / 2}^{k}) + w_{n}^{k + n / 2} C (w_{n / 2}^{k}) \\ = B (w_{n / 2}^{k}) - w_{n}^{k} C (w_{n / 2}^{k}) \end{aligned}

IDFT(逆离散傅里叶变换)

将多项式的点值表示 $(w_{n}^{k}, b_{k})$ , $(k = 0, 1, \dots, n - 1)$ 转化为其系数表示 $A (x) = a_{0} + a_{1} x + \dots + a_{n - 1} x^{n - 1}$

我直接给出逆变换的公式 $a_{i} = \frac{1}{n} \sum_{k = 0}^{n - 1} b_{k} w_{n}^{- i k}$

但是现在要思考如何理解这个公式

对于上面那个 DFT 的变换的矩阵

A Ω = D

现在相当于已知 $Ω$ 和 $D$ 求 $A$ ，那么只需要求出 $Ω^{- 1}$ 即可

尝试构造 $Ω^{- 1}$ ，我们尝试共轭矩阵 $\overset{―}{Ω}$

\begin{array}{r} Ω \cdot \overset{―}{Ω} = P = (\begin{array}{c} w_{n}^{0 \times 0} & w_{n}^{0 \times 1} & w_{n}^{0 \times 2} & \dots & w_{n}^{0 \times (n - 1)} \\ w_{n}^{1 \times 0} & w_{n}^{1 \times 1} & w_{n}^{1 \times 2} & \dots & w_{n}^{1 \times (n - 1)} \\ w_{n}^{2 \times 0} & w_{n}^{2 \times 1} & w_{n}^{2 \times 2} & \dots & w_{n}^{2 \times (n - 1)} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ w_{n}^{(n - 1) \times 0} & w_{n}^{(n - 1) \times 1} & w_{n}^{(n - 1) \times 2} & \dots & w_{n}^{(n - 1) \times (n - 1)} \end{array}) (\begin{array}{c} w_{n}^{- 0 \times 0} & w_{n}^{- 0 \times 1} & w_{n}^{- 0 \times 2} & \dots & w_{n}^{- 0 \times (n - 1)} \\ w_{n}^{- 1 \times 0} & w_{n}^{- 1 \times 1} & w_{n}^{- 1 \times 2} & \dots & w_{n}^{- 1 \times (n - 1)} \\ w_{n}^{- 2 \times 0} & w_{n}^{- 2 \times 1} & w_{n}^{- 2 \times 2} & \dots & w_{n}^{- 2 \times (n - 1)} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ w_{n}^{- (n - 1) \times 0} & w_{n}^{- (n - 1) \times 1} & w_{n}^{- (n - 1) \times 2} & \dots & w_{n}^{- (n - 1) \times (n - 1)} \end{array}) \end{array}

观察答案矩阵 $P$ 的第 $i$ 行第 $i$ 列

P = \sum_{k = 0}^{n - 1} w_{n}^{i \times k} w_{n}^{- k \times j} = \sum_{k = 0}^{n - 1} w_{n}^{(i - j) \times k}

我们发现这是一个公差为 $w_{n}^{i - j}$ 的等差数列求和，根据等差数列求和公式

\sum_{k = 0}^{n - 1} w_{n}^{(i - j) \times k} = {\begin{cases} n, i = j \\ \frac{1 - (w_{n}^{i - j})^{n}}{1 - w_{n}^{i - j}} = 0, i \neq j \end{cases}

得出答案矩阵为：

(\begin{matrix} n & 0 & 0 & \dots & 0 \\ 0 & n & 0 & \dots & 0 \\ 0 & 0 & n & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & 0 & \dots & n \end{matrix}) = n I

$Ω \cdot \overset{―}{Ω} = n I$ ， $Ω^{- 1} = \frac{1}{n} \overset{―}{Ω}$

这样就可以求出 $D = \frac{1}{n} \overset{―}{Ω} A$ ，也就是我们上面的公式

a_{i} = \frac{1}{n} \sum_{k = 0}^{n - 1} b_{k} w_{n}^{- i k}

现在我们已知了 DFT 和 IDFT 的公式，那么我们就可以进行 FFT 了

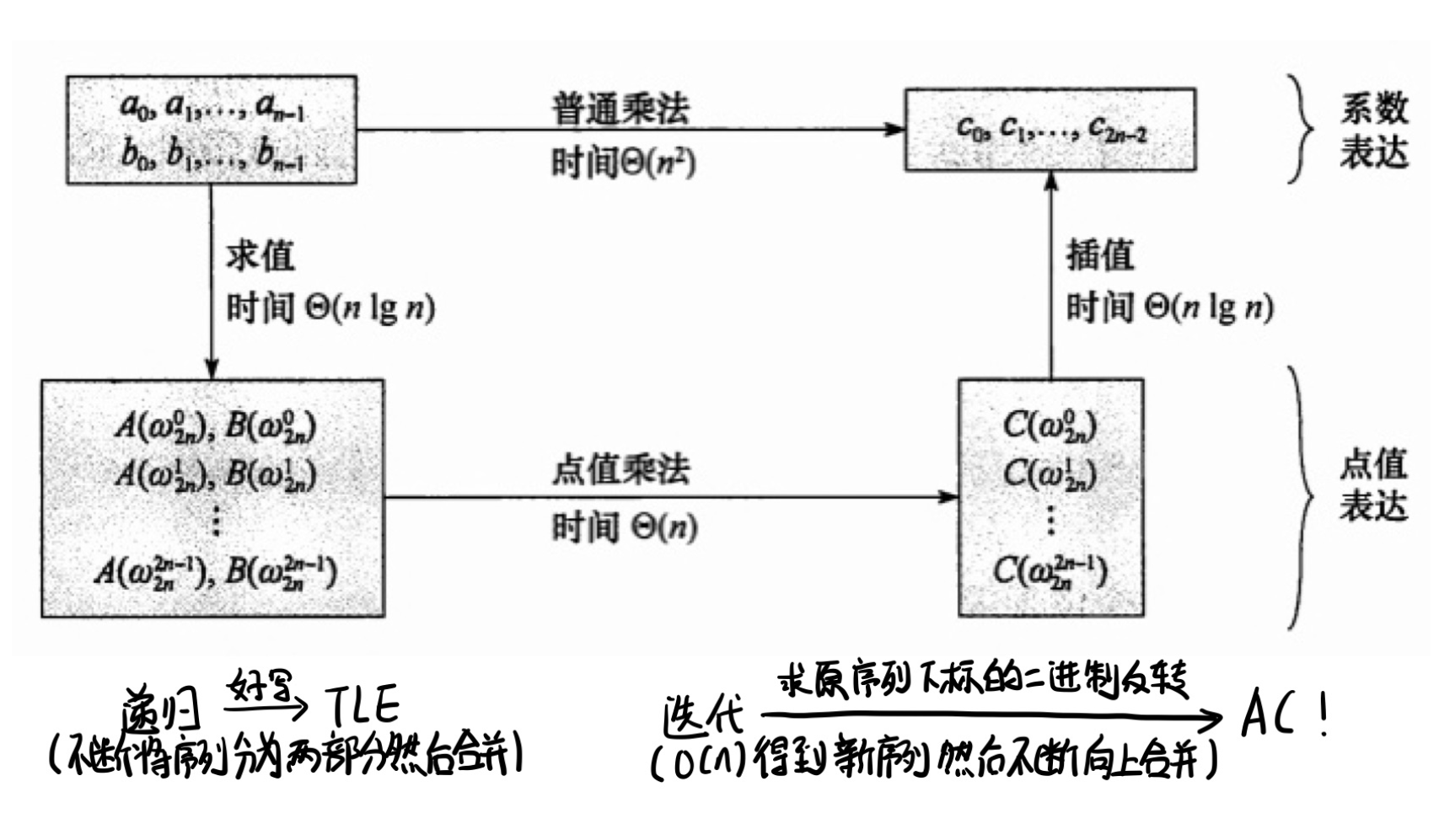
直接来看代码实现

首先，我们需要一个复数类，尽管 C++ 有复数类，常数太大了

struct Complex {
    double x, y;
    Complex (double x = 0, double y = 0) : x(x), y(y) {}
};

Complex operator + (Complex a, Complex b) { return Complex(a.x + b.x, a.y + b.y); }
Complex operator - (Complex a, Complex b) { return Complex(a.x - b.x, a.y - b.y); }
Complex operator * (Complex a, Complex b) { return Complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x); }

递归实现 FFT

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1 << 22;
const double eps = 1e-6, pi = acos(-1);

complex<double> a[MAXN], b[MAXN], c[MAXN];
int n, m;

void FFT(complex<double> *a, int n, int inv) { // inv 为 1 时为 FFT, inv 为 -1 时为 IFFT
    if (n == 1) return;
    int mid = n >> 1;
    complex<double> A1[mid + 1], A2[mid + 1];
    for (int i = 0; i <= n; i += 2) {
        A1[i >> 1] = a[i];
        A2[i >> 1] = a[i + 1];
    }
    FFT(A1, mid, inv); FFT(A2, mid, inv);
    complex<double> w0(1, 0), wn(cos(2 * pi / n), inv * sin(2 * pi / n));
    for (int i = 0; i < mid; i++, w0 *= wn) {
        a[i] = A1[i] + w0 * A2[i];
        a[i + mid] = A1[i] - w0 * A2[i];
    }
}

int main() {
    scanf("%d %d", &n, &m);
    for (int i = 0; i <= n; i++) {double x; scanf("%lf", &x); a[i].real(x);}
    for (int i = 0; i <= m; i++) {double x; scanf("%lf", &x); b[i].real(x);}
    int len = 1 << max((int)ceil(log2(n + m)), 1); //由于FFT需要项数为2的整数次方倍，所以多项式的次数len为第一个大于 n+m 的二的正整数次方
    FFT(a, len, 1); FFT(b, len, 1);
    for (int i = 0; i < len; i++) c[i] = a[i] * b[i];
    FFT(c, len, -1);
    for (int i = 0; i <= n + m; i++)
        printf("%.0f ",(c[i].real() / len + eps));
    return 0;
}

蝴蝶变换

观察原序列和后序列的二进制之后，惊奇的发现，其实际上就是把二进制翻转了，我们可以用 $O (32 n)$ 来实现

实际上可以用 $O (n)$ 的递推式来实现，定义 $R (n)$ 表示 $n$ 二进制反转后对应的值，有递推式：

R (n) = R (n / 2) + (n & 1) \times \frac{n}{2}

通过这个递推式能求出 $R (n)$

void change(complex<double> A[], int n) {
    for (int i = 0; i < n; i++)
        R[i] = (R[i >> 1] >> 1) + ((i & 1) ? n >> 1 : 0);
    for (int i = 0; i < n; i++)
        if (i < R[i]) swap(A[i], A[R[i]]); // 只需要换一次
}

然后有了这个思路，就可以直接构造出最后一层的下标然后从下往上模拟递归合并的过程了

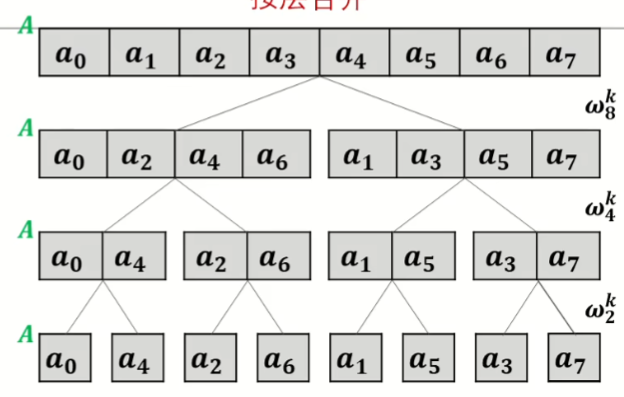
#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1 << 22;
const double eps = 1e-6, pi = acos(-1);

complex<double> a[MAXN], b[MAXN], c[MAXN];
int R[MAXN];
int n, m;

void change(complex<double> A[], int n) {
    for (int i = 0; i < n; i++)
        R[i] = (R[i >> 1] >> 1) + ((i & 1) ? n >> 1 : 0);
    for (int i = 0; i < n; i++)
        if (i < R[i]) swap(A[i], A[R[i]]);
}

void FFT(complex<double> *a, int n, int inv) { // inv 为 1 时为 FFT, inv 为 -1 时为 IFFT
    change(a, n);
    for (int m = 2; m <= n; m <<= 1) {
        complex<double> w1(cos(2 * pi / m), inv * sin(2 * pi / m));
        for (int i = 0; i < n; i += m) {
            complex<double> wk(1, 0);
            for (int j = 0; j < m / 2; j++, wk *= w1) {
                auto x = a[i + j], y = wk * a[i + j + m / 2];
                a[i + j] = x + y; a[i + j + m / 2] = x - y;
            }
        }
    }
}

int main() {
    scanf("%d %d", &n, &m);
    for (int i = 0; i <= n; i++) {double x; scanf("%lf", &x); a[i].real(x);}
    for (int i = 0; i <= m; i++) {double x; scanf("%lf", &x); b[i].real(x);}
    int len = 1 << max((int)ceil(log2(n + m)), 1); //由于FFT需要项数为2的整数次方倍，所以多项式的次数len为第一个大于 n+m 的二的正整数次方
    FFT(a, len, 1); FFT(b, len, 1);
    for (int i = 0; i < len; i++) c[i] = a[i] * b[i];
    FFT(c, len, -1);
    for (int i = 0; i <= n + m; i++)
        printf("%.0f ",(c[i].real() / len + eps));
    return 0;
}

NTT

原根

欧拉定理

若正整数 $m, a$ ，满足 $gcd (a, m) = 1$ ，则 $a^{φ (n)} \equiv 1 (\mod m)$

阶

若正整数 $m, a$ ，满足 $gcd (a, m) = 1$ ，则 $a^{k} \equiv 1 (\mod m)$ 的最小正整数 $k$ 称为 $a$ 对模 $m$ 的阶，记作 $δ_{m} (a)$

若 $δ_{m} (a) = φ (m)$ ，则称 $a$ 为 $m$ 的一个原根

阶的性质

假设 $(a, m) = 1, δ = δ_{m} (a)$ ，则

$a^{0}, a^{1}, \dots, a^{δ - 1}$ 在模 $m$ 意义下两两不同
$a^{γ} \equiv a^{γ^{'}} (\mod m) \Leftrightarrow γ \equiv γ^{'} (\mod m)$
$δ | φ (m)$

原根的存在与判定

只有模 $2, 4, p^{a}, 2 p^{a}$ 存在原根（ $p$ 是奇质数）

原根的判定定理

设 $m > 1$ ， $g$ 为正整数且 $(g, m) = 1$ 。则 $g$ 是 $m$ 的原根当且仅当对于任意 $φ (m)$ 的质因子 $q_{i}$ ， $g^{\frac{φ (m)}{q_{i}}} ≢ 1 (\mod m)$

如何寻找原根，假设这里我们需要寻找 $p$ 的原根，那么有 $g^{0}, g^{1}, \dots, g^{φ (p) - 1}$ 在模 $p$ 意义下各不相同，如果 $p$ 是一个质数，那么这里有 $φ (p) = p - 1$

一个数原根的个数为 $φ (φ (p))$ 但是第一个原根往往不是特别大，所以从小到大枚举 $r t$ 然后 $O (p)$ 去 check

若 $r t$ 不是原根，那么一定存在 $0 \leq i < j \leq φ (n) - 1$ 使得 $g^{i} \equiv g^{j} (\mod p)$ 那么有 $g^{j - i} \equiv 1 (\mod p)$ ，所以说如果出现一个 $0 < d = j - i < φ (p)$ 使得 $g^{d} \equiv 1 (\mod p)$ ，那么就说明 $r t$ 不是原根

int rt = 1; // P 是一个质数
while (true) {
    bool ok = true;
    int v = 1;
    for (int i = 1; i < P - 1; i++) {
        v = v * rt % P;
        if (v == 1) {
            ok = false;
            break;
        }
    }
    if (ok) break;
    rt += 1;
}

设 $d = j - i$ ，又有 $g^{φ (n)} \equiv 1 (\mod p)$ ，所以有 $d | φ (n)$

于是，我们只需要预处理出 $φ (n)$ 的的因数 ${e}$ ，对于一个 $r t$ 如果存在一个 $r t^{e_{i}} \equiv 1 (\mod p)$ 那么 $r t$ 就不是原根

指标

对于质数 $p$ ，假设 $g$ 是 $p$ 的一个原根，则 $g^{0}, g^{1}, g^{p - 2}$ 在模 $p$ 意义下是 $1, 2, \dots, p - 1$ 的一个排列。假设对于 $1 \leq x \leq p - 1$ 有 $g^{c} \equiv x (\mod p)$ 则称 $x$ 的指标为 $c$ ，记作 $ind (x) = c$

指标有着非常优秀的性质，也被称为离散对数： $\forall 1 \leq x, y < p, ind (x y) \equiv ind (x) + ind (y) (\mod φ (p)))$

如何求一个 $ind (x)$ 可以使用 BSGS 算法

求所有的 $ind(x)$ 可以使用 $O (n)$ 的递推

vector<ll> lg(P, 0);
for (int i = 0, v = 1; i < P - 1; i++) {
    lg[v] = i;
    v = v * rt % P;
}

NTT 实现

假设质数 $p = r 2^{l} + 1$ ， $g$ 是 $p$ 的原根，和 FFT 类似，我们用 $g_{n} = g^{\frac{p - 1}{n}}$ 代替 $w_{n}$

我们发现，这样子去选取 $g_{n}$ 一样满足一些性质：

$g_{2 n}^{2 k} \equiv g_{n}^{k} (mod p), (2 n \leq 2^{l})$
$g_{2 n}^{n} \equiv - 1 (mod p), (2 n \leq 2^{l})$
$\sum_{k = 0}^{n - 1} g_{n}^{i k} g_{n}^{- k j} \equiv {\begin{cases} n, if i = j \\ 0, otherwise \end{cases}$

和 FFT 类似，只不过这里用原根来替换单位根，来进行一个模意义下的运算，FFT 中的 DFT，IDFT，依然成立

NTT 的优点：快，精确
NTT 的限制：模数需要是满足 $p = r 2^{l} + 1$ 的质数 $p$ ，

下面有些常见的模数：

$65537 = 2^{16} + 1, g = 3$
$998244353 = 119 \times 2^{23} + 1, g = 3$
$1004535809 = 479 \times 2^{21} + 1, g = 3$
$4179340454199820289 = 29 \times 2^{57} + 1, g = 3$

非递归的 NTT

//NTT

int rev[MAXN], limit, bit;

void NTT (vector<ll> &a, int op) {
    for (int i = 0; i < limit; i++)
        if (i < rev[i]) swap(a[i], a[rev[i]]);
    
    for (int m = 2; m <= limit; m <<= 1) {
        ll gn = qpow(3, (MOD - 1) / m); 
        if (op == -1) gn = qpow(gn, MOD - 2);
        for (int i = 0; i < limit; i += m) {
            ll gk = 1;
            for (int j = 0; j < m / 2; j++) {
                ll x = a[i + j], y = gk * a[i + j + m / 2] % MOD;
                a[i + j] = (x + y) % MOD;
                a[i + j + m / 2] = (x - y + MOD) % MOD;
                gk = gk * gn % MOD;
            }
        }
    }
}

void convolution(vector<ll> A, vector<ll> B, vector<ll> &C) {
    int n = A.size() - 1, m = B.size() - 1;
    limit = 1, bit = 0;
    while (limit <= n + m) limit <<= 1, bit += 1;
    for (int i = 0; i < limit; i++)
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));

    A.resize(limit), B.resize(limit); C.resize(limit);
    for (int i = n + 1; i < limit; i++) A[i] = 0;
    for (int i = m + 1; i < limit; i++) B[i] = 0;
    
    NTT(A, 1), NTT(B, 1);


    for (int i = 0; i < limit; i++)
        C[i] = A[i] * B[i] % MOD;
    NTT(C, -1);
    ll inv = qpow(limit, MOD - 2);
    for (int i = 0; i < limit; i++)
        C[i] = C[i] * inv % MOD;
}

牛顿迭代

给定多项式 $g (x)$ ，求满足 $g (f (x)) = 0 (\mod x^{n})$ 的形式幂级数 $f (x)$

当 $n = 1$ 时， $[x^{0}] g (f (x)) = 0$ 可以求出

假设现在已经得到了 $(\mod x^{⌈ \frac{n}{2} ⌉})$ 的解 $f_{0} (x)$

有递归式：

f (x) \equiv f_{0} (x) - \frac{g (f_{0} (x))}{g^{'} (f_{0} (x))} (\mod x^{n})

多项式求逆

给定函数 $h (x)$ ，有方程

g (f (x)) = \frac{1}{f (x)} - h (x) \equiv 0 (\mod x^{n})

应用牛顿迭代可得：

\begin{aligned} f (x) & \equiv f_{9} (x) - \frac{\frac{1}{f_{0} (x)} - h (x)}{- \frac{1}{f_{0}^{2} (x)}} \\ \equiv 2 f_{0} (x) - f_{0}^{2} (x) h (x) \end{aligned}

于是，我们就得到了 $f (x)$ 的递推是

根据主定理，时间复杂度为 $O (n \log n)$

多项式开方

设给定函数为 $h (x)$ 有方程：

g (f (x)) = f^{2} (x) - h (x) \equiv 0 (\mod x^{n})

应用牛顿迭代可得：

\begin{aligned} f (x) & \equiv f_{0} - \frac{f_{0}^{2} (x) - h (x)}{2 f_{0} (x)} (\mod x^{n}) \\ \equiv \frac{f_{0}^{2} (x) + h (x)}{2 f_{0} (x)} (\mod x^{n}) \end{aligned}

时间复杂度 $O (n \log n)$

多项式 exp

给定函数 $h (x)$ ，有方程：

g (f (x)) = \ln f (x) - h (x) (\mod x^{n})

应用牛顿迭代可得：

\begin{aligned} f (x) & \equiv f_{0} (x) - \frac{\ln f_{0} (x) - h (x)}{\frac{1}{f_{0} (x)}} (\mod x^{n}) \\ \equiv f_{0} (x) (1 - \ln f_{0} (x) + h (x)) (\mod x^{n}) \end{aligned}

时间复杂度为 $O (n \log n)$

拉格朗日差值

$n$ 个点值 $(x_{i}, y_{i}), (1 \leq i \leq n)$ ，满足 $x_{i} \neq x_{j}, (i \neq j)$ ，它们唯一确定一个 $n - 1$ 次多项式 $f (x)$

f (x) = \sum_{i = 1}^{n} y_{i} \prod_{j \neq i} \frac{x - x_{j}}{x_{i} - x_{j}}

拉格朗日差值定理用于点值表示转化成多项式形式，我们需要构造出一个多项式，满足 $f (x_{i}) = y_{i}$

首先，把 $f (x)$ 拆成 $n$ 个函数相加的形式 $f (x) = f_{1} (x) + f_{2} (x) + \dots + f_{n} (x)$

特别的，我们可以令 $f_{i} (x)$ 当且仅当在 $x = x_{i}$ 时 $f (x_{i}) = y_{i}$ ，其他时候都为 $0$

那么很显然可以构造出 $f_{i} (x) = A \prod_{i \neq j} (x - x_{j})$ ，其中 $A$ 是一个系数，我们把 $f_{i} (x_{i}) = y_{i}$ 带入

\begin{aligned} f_{i} (x_{i}) = A \prod_{i \neq j} (x_{i} - x_{j}) = y_{i} \\ ⟺ & A = \frac{y_{i}}{\prod_{i \neq j} (x_{i} - x_{j})} \end{aligned}

回代：

f_{i} (x) = \frac{y_{i}}{\prod_{i \neq j} (x - x_{j})} \prod_{i \neq j} (x - x_{j}) = y_{i} \prod_{i \neq j} \frac{x - x_{j}}{x_{i} - x_{j}}

则：

f (x) = \sum_{i = 1}^{n} f_{i} (x) = \sum_{i = 1}^{n} y_{i} \prod_{j \neq i} \frac{x - x_{j}}{x_{i} - x_{j}}

考虑计算

特殊情况一：

只需要求一个 $f (x_{0})$ ，那么暴力 $O (n^{2})$ 算即可

特殊情况二：

只需要求一个 $f (x_{o})$ ，并且满足 $x_{i} = i$ ，是可以优化到 $O (n)$ 的