20.莫队

莫队

转载大佬的博客

引入

当如果知道区间 $[L, R]$ 的答案，如果能 $O (1)$ 地求出 $[L - 1, R], [L, R - 1] \dots$ 相邻的区域的答案，那么，就可以考虑莫队

莫队算法 $=$ 离线 $+$ 暴力 $+$ 分块

莫队时一种离线算法，他通常用于不修改只查询的一类区间问题，复杂度为 $O (n \sqrt{n})$ ，没有在线算法线段树或树状数组好，但是胜在好写

思考一个问题，

给定一个序列，和 $m$ 组询问，每次询问 $[L, R]$ 区间内不同的数有几个

考虑暴力做法，我们定义两个指针 $L, R$ ，假设我们已经知道了 $[L, R]$ 的答案，我们可以平移指针来 $O (1)$ 得到下一位置的答案，例如 $[L + 1, R], [L, R + 1], \dots$

我们可以从 $L = 1, R = 1$ 开始平移 $n$ 次来得到任意区间 $[L, R]$ 的答案，对于多组询问，我们可以把询问按照左结点排序，就相当于右节点一直反复跑，左节点向右移

显然，我们可以造一组恶心的数据把这样的想法卡死，每次右节点跑 $n$ 次， $m$ 组询问，总的时间复杂度为 $O (n m)$ ，那么有没有什么办法能找一个询问的排序方案使得时间复杂度更优秀呢？答案是有的

暴力法几何解释

我们考虑用几何来解释区间和区间之间的连线，我们把区间 $L, R$ 定义成坐标轴上的点 $x = L, y = R$ ，两个区间之间的距离就是对应的两个点之间的距离的哈夫曼距离

$(a)$ 情况中的区间是 $(2, 6) \Rightarrow (4, 8)$ ， $(b)$ 情况中的区间是 $(2, 9) \Rightarrow (3, 5)$

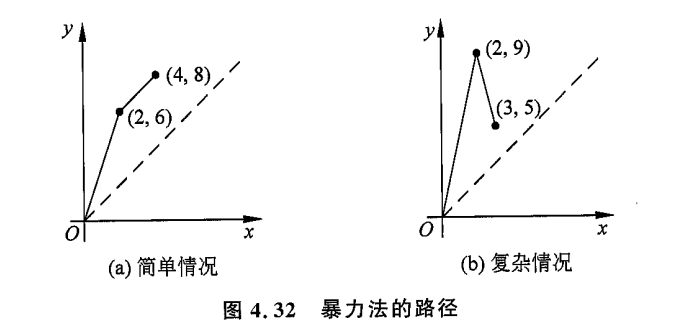
莫队算法

把数组分块，然后把查询的区间按左端点所在的块排序，如果左端点相同，再按右端点排序

莫队算法的几何解释

莫队算法把 $x$ 轴分成了多个块，每个区块内按照 $y$ 坐标排序，一个区块处理完了再进入下一个区块，这样就形成了一条比较短的路径，从而降低了时间复杂度

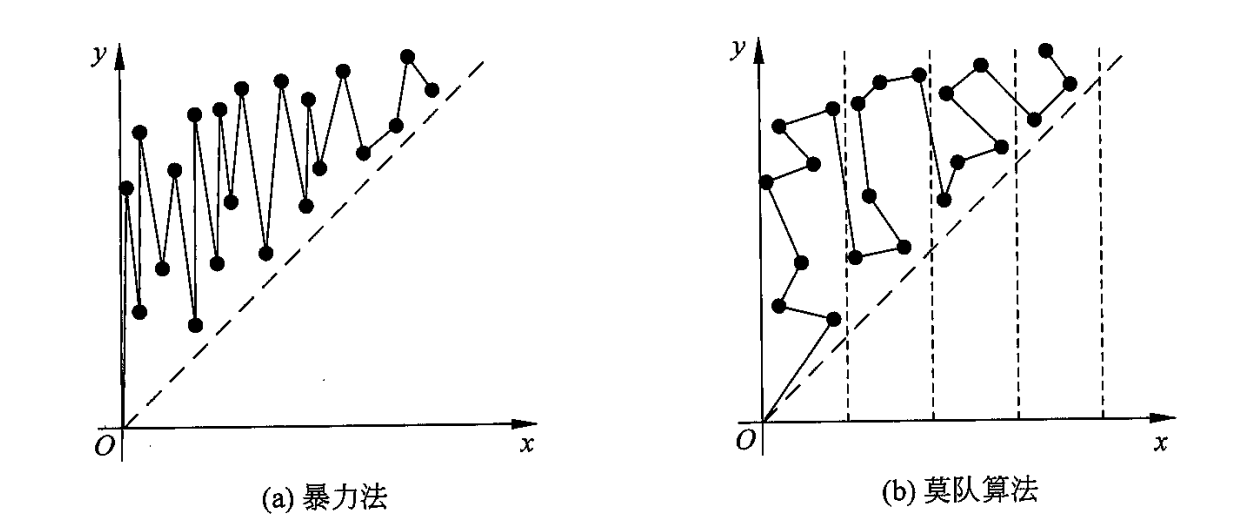
考虑 $x$ 方向上的复杂度，在一个区块内，沿着 $x$ 方向一次移动最多 $\sqrt{n}$ 个单位，区块共有 $m$ 个，总时间复杂度为 $O (m \sqrt{n})$

考虑 $y$ 方向上的时间复杂度，每个区块内，验证 $y$ 方向单向移动，整个区块内的 $y$ 方向长度为 $n$ ，有 $\sqrt{n}$ 个区块，总时间复杂度为 $n \sqrt{n}$

两者相加，总时间复杂度为 $O (m \sqrt{n} + n \sqrt{n})$ 当 $m, n$ 同阶时，复杂度为 $O (n \sqrt{n})$

#include<bits/stdc++.h>
using namespace std;
const int MAXX=1e6;
struct node{
    int L,R,id;
    node(int L=0,int R=0,int id=0):L(L),R(R),id(id){}
};

int now_ans=0;
vector<int> a,belong,ans,cnt;
vector<node> q;

bool cmp(node a,node b){
    if(belong[a.L]!=belong[b.L]) return belong[a.L]<belong[b.L];
    return a.R<b.R;
}

void add(int x){cnt[a[x]]++;if(cnt[a[x]]==1) now_ans++;}
void del(int x){cnt[a[x]]--;if(cnt[a[x]]==0) now_ans--;}

int main(){
    freopen("P1972.in","r",stdin);
    freopen("P1972.out","w",stdout);
    int n;scanf("%d",&n);
    int block=sqrt(n),t=n/block+(n%block!=0);
    a.assign(n+1,0);belong.assign(n+1,0);ans.assign(n+1,0);cnt.assign(MAXX+1,0); 
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),belong[i]=(i-1)/block+1;
    int m;scanf("%d",&m);q.assign(m+1,node());
    for(int i=1;i<=m;i++){
        int L,R;scanf("%d%d",&L,&R);
        q[i]=node(L,R,i);
    }
    sort(q.begin()+1,q.begin()+1+m,cmp);
    int L=1,R=0;
    for(int i=1;i<=m;i++){
        while(L<q[i].L) del(L++);
        while(R>q[i].R) del(R--);
        while(L>q[i].L) add(--L);
        while(R<q[i].R) add(++R);
        ans[q[i].id]=now_ans;
    }
    for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
    return 0;
}

$P 1972$ 这道题数据莫队时过不了的www

莫队可以有些小优化，就是对于编号为奇数的块按照 $R$ 从小到大排序，编号为偶数的块按照 $R$ 从大到小表示

这个优化在图上也很显然能表示出来，从奇数点 $y$ 坐标从小到大，然后偶数的 $y$ 坐标从大到小，这样走能省掉一个块走完然后立马从 $y$ 的高点到 $y$ 的低点的过程

带修改的莫队

如果上面那个问题再添加一个修改操作

R x val 表示把第 $x$ 位置上的数改成 $v a l$

我们可以按照修改把询问 $m$ 拆成几部分，然后一部分给一个时间维度 $t$

不修改的是二维平面上的点 $(x, y)$ ，那么加上时间维度就是三维平面上一个点 $(x, y, t)$

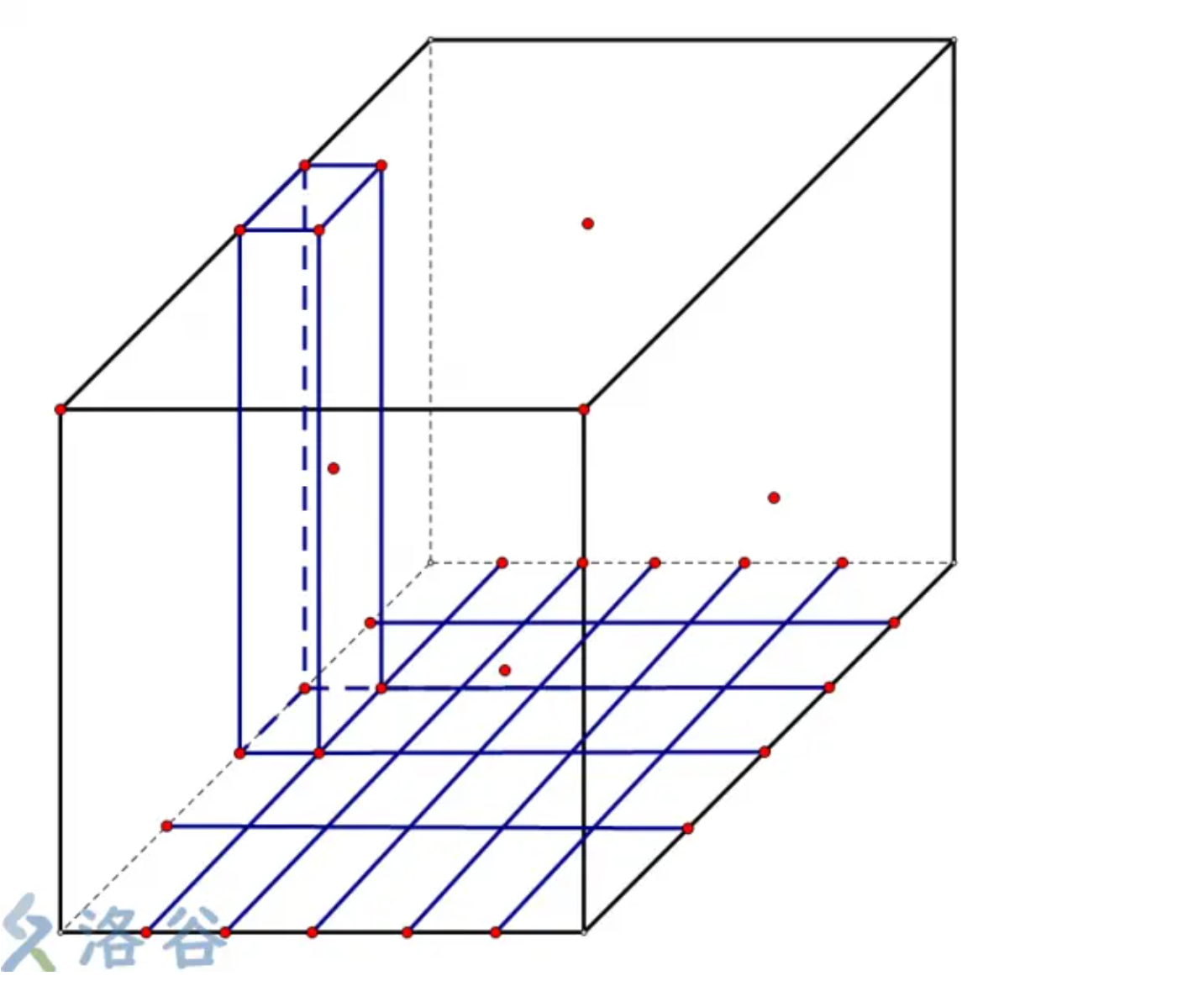
就变成了在三维平面上选一条路径使得曼哈顿距离尽量小

依旧采用分块的办法，先按照左端点 $L$ 排序，左端点 $L$ 在同一个块，按照右端点排序，如果右端点在同一个块，就按照之间维度 $t$ 排序

那么块的大小取多少最好呢，不妨设块的大小为 $B$

$x$ 方向上的复杂度。在一个区块内，沿着 $x$ 方向一次最多移动 $B$ ，所有的区块公用 $m$ 次移动，总计算量为 $m B$
$y$ 方向上的复杂度。和 $x$ 一样，总复杂度为 $m B$
$z$ 方向上的复杂度，，每个被 $x$ 和 $y$ 区块限制的方格内，沿着 $z$ 方向单向移动最多 $m$ 次（询问的次数）总共有 $\frac{n^{2}}{B^{2}}$ 个方格，总计算量为 $m n^{2} / B^{2}$

总时间复杂度为 $O (m B + m n^{2} / B^{2})$ 。当 $B = n^{\frac{2}{3}}$ 时有较好的复杂度 $O (m n^{\frac{2}{3}})$