K-D Tree

一般的二叉树只能在每个节点上表示一个数据，如果需要在一个节点上表示多个数据，可以用 K-D 树

先假设维度是二维，那么先对 $x$ 进行划分，分为左右两部分，求 $x$ 的中位数 $mid$ 作为根，把 $x<mid$ 的节点给左子树，$x>mid$ 的节点给右子树

然后再对 $y$ 进行划分，每个子树分成两部分 ，取每个子树中 $y$ 的中位数 $mid$ ，把 $y<mid$ 的节点给左子树，$y>mid$ 的节点给右子树

第三次对 $x$ 进行划分，第四次对 $y$ 进行划分，以此类推...

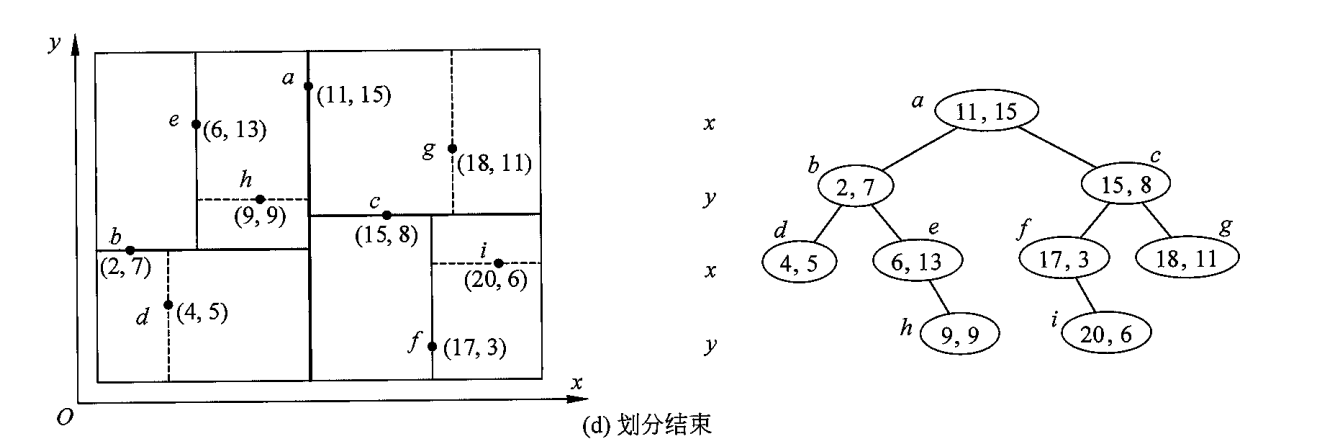
这种划分的方式叫做轮转法，即有 $k$ 维，$1\cdots k$ 第 $i$ 次划分第 $(i-1)\mathrm{\%}k+1$ 维

还有一种划分方式，叫做最大方差法，适用于某些维度的值变化不大的情况，例如二维平面中 $x$ 均匀分布，$y$ 相差不大，$n$ 个点再平面上呈一条横先，此时按照 $y$ 划分没有太大意义，可以每次都按 $x$ 划分，具体操作就是每次划分时，选择方差最大的维度进行划分，方差的定义为 $s^2=\frac{1}{n}\sum _{i=0}^{n-1}(x_i-\mu {)}^2$

建树

如果预先给定了 $n$ 个数据，那么用递归建就可以了

struct Point{
    LL dim[K];
};
Point q[maxn],t[maxn];

int now;

bool cmp(const Point &a,const Point &b){
    return a.dim[now] < b.dim[now];
}

void build(int L,int R,int dep){
    if(L > R) return ;
    int d = dep % K, mid = (L+R)/2; now = d;
    nth_element(t+L,t+mid,t+R+1,cmp);
    build(L,mid-1,dep+1); build(mid+1,R,dep+1);
}

插入

插入新节点，按照 K-D 树的规则，在 K-D 树上找到需要插入的位置，然后插入

如果发现不平衡，可以利用替罪羊树，推倒重建

删除

同理，也可以使用替罪羊树的删除方法，替罪羊树可以看成是一维的 K-D 树，K-D 树是替罪羊树的拓展