20.树状数组

树状数组

树状数组用于维护和查询区间前缀和

二进制编码

树状数组时利用数的二进制特征进行检索的一种树状的结构

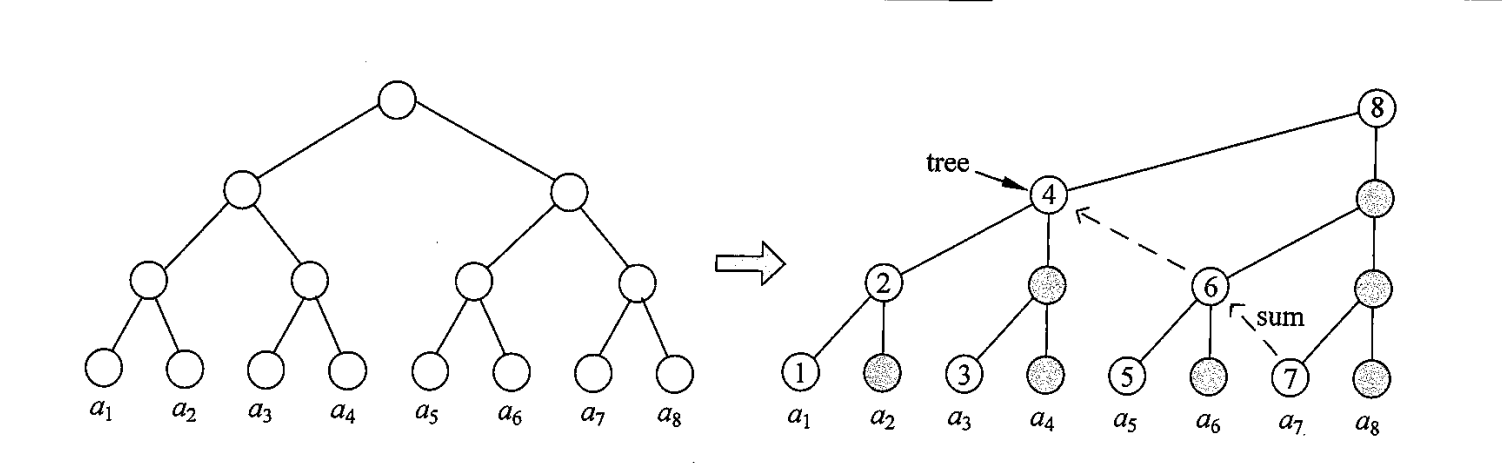
我们发现，圈里带数字的节点我们定义为 $t [x]$ ，一个节点上的 $t [x]$ 定义为其树下直练的子节点的和，例如 $t [8] = t [4] + t [6] + t [7] + a_{8}$

这样子我们就能把前缀和的查询控制在 $O (\log n)$ 了

考虑维护，我们发现当有一个 $a_{i}$ 改变时，需要改变的 $t [x]$ 就是 $a_{i}$ 的祖先节点，也就是 $O (\log n)$ 的复杂度

观察发现，查询操作实际上是每次去掉二进制下的最后一个 $1$ ，例如： $s u m (7) = t [7] + t [6] + t [4]$ ，也就是 $s u m ((111)_{2}) = t [(111)_{2}] + t [(110)_{2}] + t [(100)_{2}]$

维护操作是每次在二进制的最后的 $1$ 加上 $1$

例如如果修改了 $a_{3}$ ，那么需要修改 $t [3], t [4], t [8]$ ，也就是 $t [(11)_{2}], t [(100)_{2}], t [(1000)_{2}]$

所以，树状数组的关键就是如何找到一个数的二进制的最后一个 $1$

我们利用负数的补码表示，可以得到二进制下的最后一个 $1$ ，也就是 $l o w b i t (x) = x & - x$

例如 $6 = (00000110)_{2}, - 6 = (11111010)_{2}, 6 & - 6 = (00000010)_{2} = 2$

惊奇的发现， $t [x]$ 数组所包括的元素个数与 $l o w b i t (x)$ 相等，也就是说， $t [x]$ 记录了 $(x - l o w b i t (x), x]$ 的元素之和

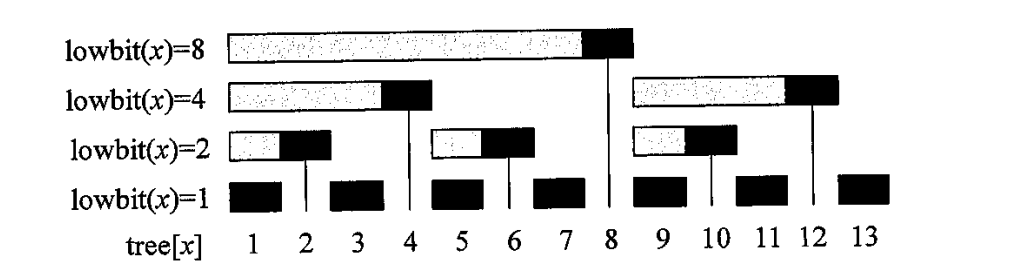
这样子利用了数的二进制下的一些特性就可以把查询优化到 $\log n$ 级别了

算法实现

单点修改+区间查询

我们很容易就能写出来

struct tree{
    int n;
    vector<int> c;
    tree(int n){this->n=n;c.assign(n+1,0);}
    void add(int x,int val){
        for(;x<=n;x+=x&-x)c[x]+=val;
    }
    int sum(int x){
        int ret=0;
        for(;x;x-=x&-x)ret+=c[x];
        return ret;
    }
}

区间修改+单点查询

我们利用前缀和的思想，如果想要在 $[L, R]$ 加上 $v a l$ 就在 $t [L] + = v a l, t [R + 1] - = v a l$ ，然后求前缀和就是答案

区间修改+区间查询

这里只用一个树状数组是做不到了，我们需要差分数组+树状数组的深度结合

求区间和 $s (L, R) = s (1, R) - s (1, L - 1)$ 问题转化为如何求 $s (1, k)$

定义 $D [x]$ 是 $a [x]$ 的差分数组，可得

\begin{aligned} a_{1} + a_{2} + \dots + a_{k} \\ = D_{1} + (D_{1} + D_{2}) + \dots + (D_{1} + D_{2} + \dots + D_{k}) \\ = k D_{1} + (k - 1) D_{2} + \dots + (k - (k - 1)) D_{k} \\ = k (D_{1} + D_{2} + \dots + D_{k}) - (0 \cdot D_{1} + 1 D_{2} + 2 D_{3} + \dots + (k - 1) D_{k}) \\ = k \sum_{i = 1}^{k} D_{i} + \sum_{i = 1}^{k} (i - 1) \cdot D_{i} \end{aligned}

就化简成了两个和式的形式，就可以用树状数组来处理了，一个实现 $D_{i}$ 一个实现 $(i - 1) D_{i}$

tree t1(n),t2(n);
    vector<int> a(n+1,0);
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++){
        int d=a[i]-a[i-1];
        t1.add_x(i,d);
        t2.add_x(i,(i-1)*d);
    }
    while(m--){
        int op;cin>>op;
        if(op==1){
            int L,R,d;cin>>L>>R>>d;
            t1.add_x(L,d);t1.add_x(R+1,-d);
            t2.add_x(L,(L-1)*d);t2.add_x(R+1,-(R+1-1)*d);
        }
        else{
            int L,R;cin>>L>>R;
            cout<<R*t1.get(R)-t2.get(R)-((L-1)*t1.get(L-1)-t2.get(L-1))<<'\n';
        }
    }

二维区间修改+区间查询

二维其实是一维的拓展，也是考虑构造差分数组 $D [i, j] = a [i, j] - a [i - 1, j] - a [i, j - 1] + a [i - 1, j - 1]$

然后需要查询 $\sum_{i = a}^{c} \sum_{i = b}^{d} a [i] [j] = \sum_{i = 1}^{c} \sum_{i = 1}^{d} a [i] [j] - \sum_{i = 1}^{c} \sum_{i = 1}^{b - 1} a [i] [j] - \sum_{i = 1}^{a - 1} \sum_{i = 1}^{d} a [i] [j] + \sum_{i = 1}^{a - 1} \sum_{i = 1}^{b - 1} a [i] [j]$

所以问题就转化为如何求 $\sum_{i = 1}^{n} \sum_{i = 1}^{m} a [i] [j]$ ，利用差分数组可得

\begin{aligned} \sum_{i = 1}^{n} \sum_{i = 1}^{m} a [i] [j] \\ = & \sum_{i = 1}^{n} \sum_{i = 1}^{m} \sum_{k = 1}^{i} \sum_{l = 1}^{j} D [k] [l] \\ = & \sum_{i = 1}^{n} \sum_{i = 1}^{m} D [i] j] \times (n - i + 1) \times (m - j + 1) \\ = & (n + 1) (m + 1) \sum_{i = 1}^{n} \sum_{i = 1}^{m} D [i] [j] - (m + 1) \sum_{i = 1}^{n} \sum_{i = 1}^{m} D [i] [j] \times i - (n + 1) \sum_{i = 1}^{n} \sum_{i = 1}^{m} D [i] [j] \times j + \sum_{i = 1}^{n} \sum_{i = 1}^{m} D [i] [j] \times i \times j \end{aligned}

所以，我们只需要构造四个树状数组来维护 $D [i] [j], D [i] [j] \times i, D [i] [j] \times j, D [i] [j] \times i \times j$ 就好了

查询和求和的复杂度都为 $O (\log n \log m)$ 但缺点是占用空间大

区间最值

其实树状数组也可以解决区间最值问题

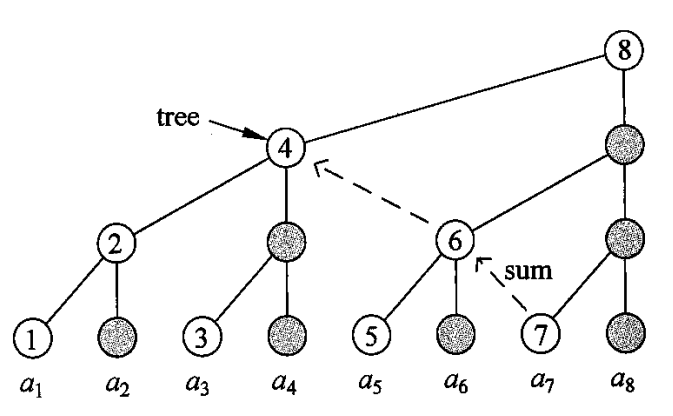
回到这个图，前缀和树状数组中， $t [x]$ 中存放的是 $(x - l o w b i t (x), x]$ 中每个数的和，那么在求最值的树状数组中就是记录的最大值

单点修改： $u p d a t e (x, v a l)$ 我们需要修改 $t [x]$ 以及 $x$ 的祖先节点

如何修改，对于祖先节点，重新求一次 $m a x$ ，也就是扫一遍每个直接的儿子节点

void update(int x,int val){
        while(x<=n){
            c[x]=val;
            for(int i=1;i<lowbit(x);i<<=1)
                c[x]=max(c[x],c[x-i]);
            x+=lowbit(x);
        }
    }

区间最值查询： $q u e r y (L, R)$

如果 $R - L \geq l o w b i t (R)$ 那么 $[L, R]$ 区间包含了 $t [R]$ 所包含的所有结点，还多出来一块 $[L, R - l o w b i t (R)]$ 则 $q u e r y (L, R) = max (t [R], q u e r y (L, R - l o w b i t (R))$
如果 $R - L \leq l o w b i t (R)$ 那么 $[L, R]$ 区间在 $t [R]$ 所包含的区间内，则往前递推 $q u e r y (L, R) = max (a [R], q u e r y (L, R - 1))$

可以写成递推的形式

int query(int L,int R){
        int ans=0;
        while(L<=R){
            ans=max(ans,a[R]);R--;
            while(R-L>=lowbit(R)){
                ans=max(ans,c[R]);
                R-=lowbit(R);
            }
        }
        return ans;
    }

更新和查询的时间复杂度都为 $O ((\log n)^{2})$