Select a result to preview

MIT18.06Linear Algebra 笔记

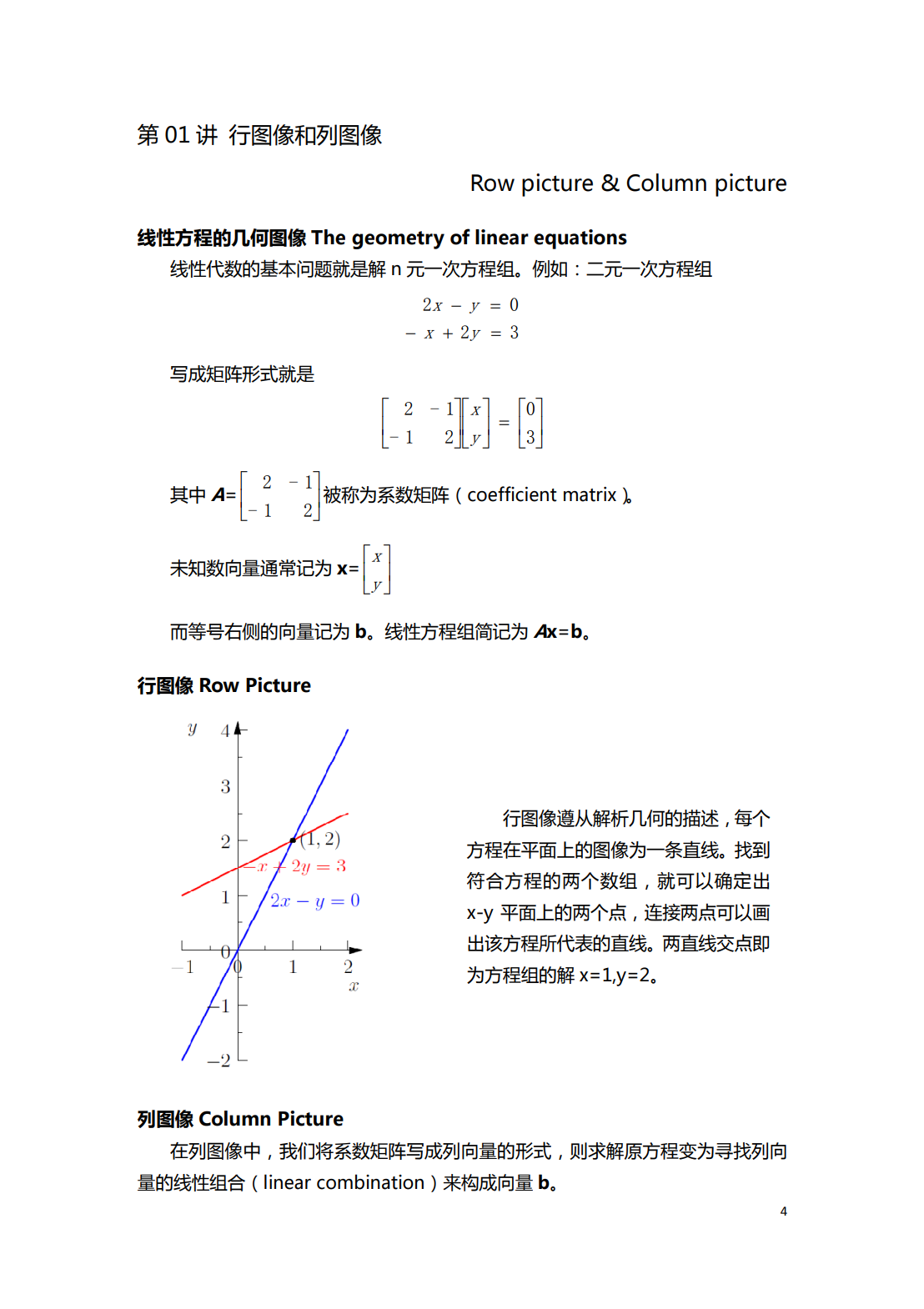
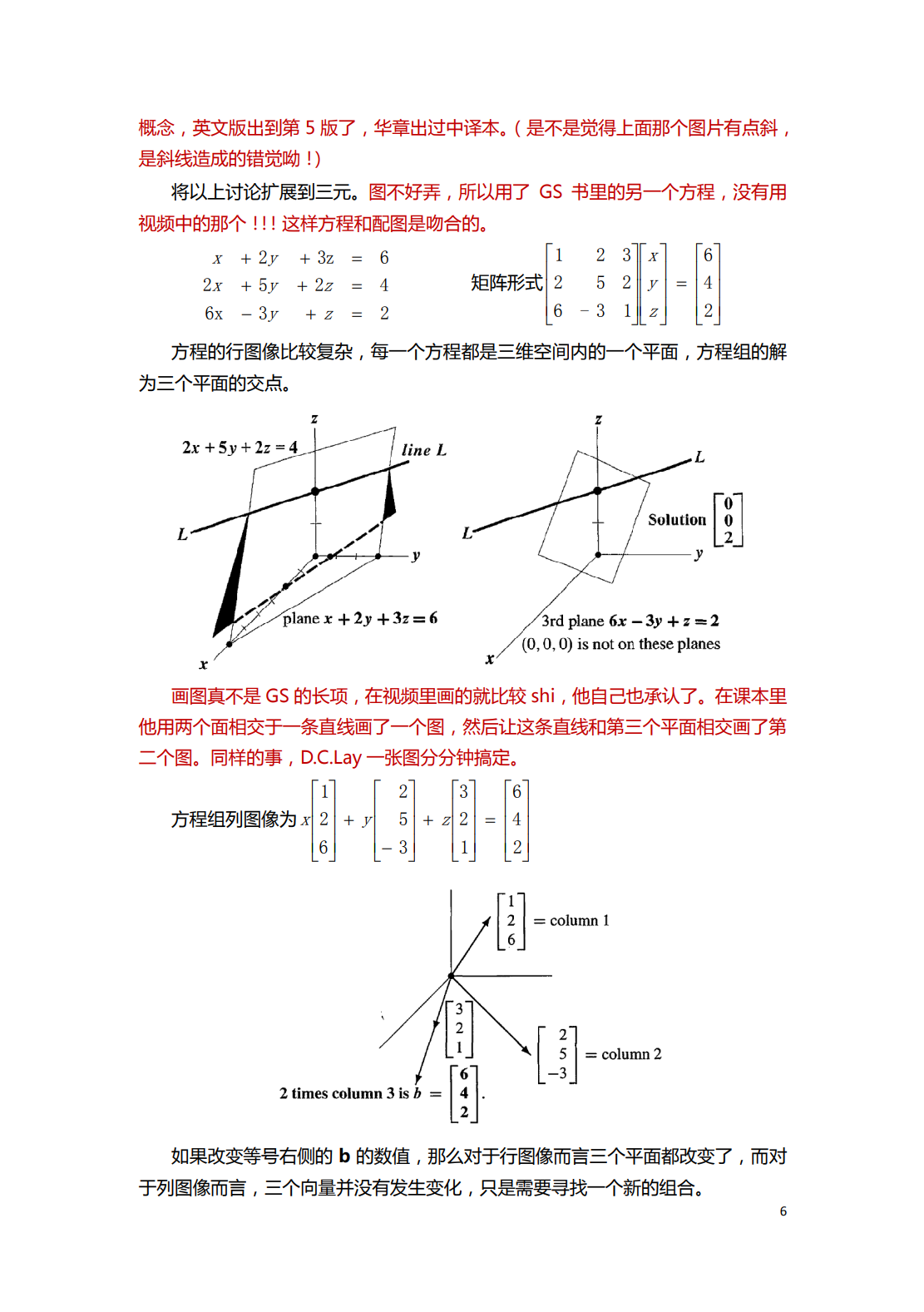
第01讲 行图像和列图像

image.png
image.png
image.png
image.png

第02讲 矩阵消元

image.png
image.png
image.png
image.png

第03讲 矩阵的乘法和逆矩阵

image.png
image.png
image.png
image.png
image.png
image.png

第04讲 矩阵的LU分解

image.png
image.png
image.png
image.png

第05讲 转置、置换和空间

image.png
image.png

第06讲 列空间和零空间

image.png
image.png

第07讲 求解Ax=0：主变量，特解

image.png
image.png

第08讲 求解Ax=b：可解性与结构

image.png
image.png
image.png

第09讲 线性无关，基和维数

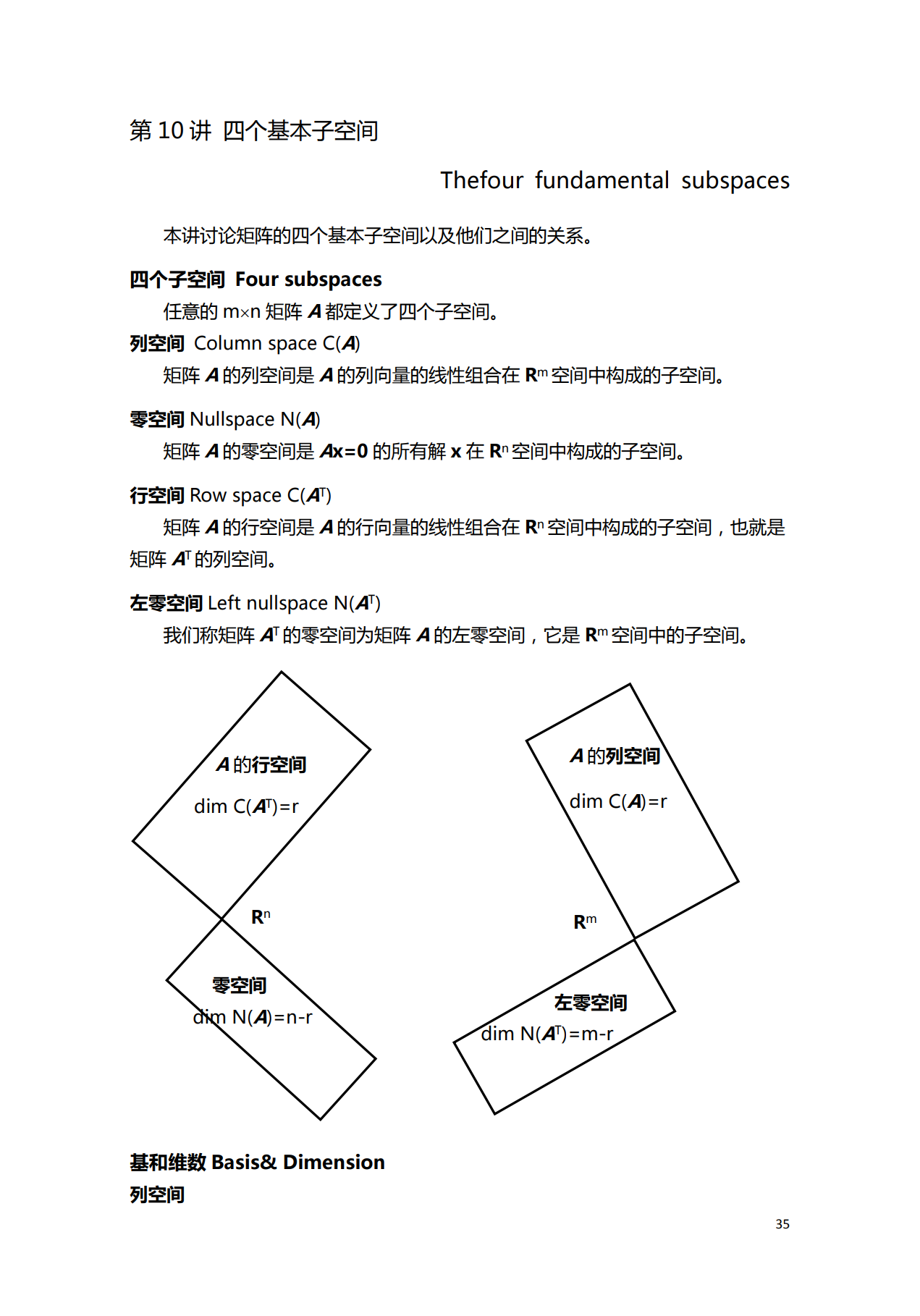
image.png
image.png
image.png

第10讲 四个基本子空间

image.png
image.png
image.png
image.png

第11讲 矩阵空间、秩 1 矩阵和小世界图

image.png
image.png
image.png

第12讲 图、网络、关联矩阵

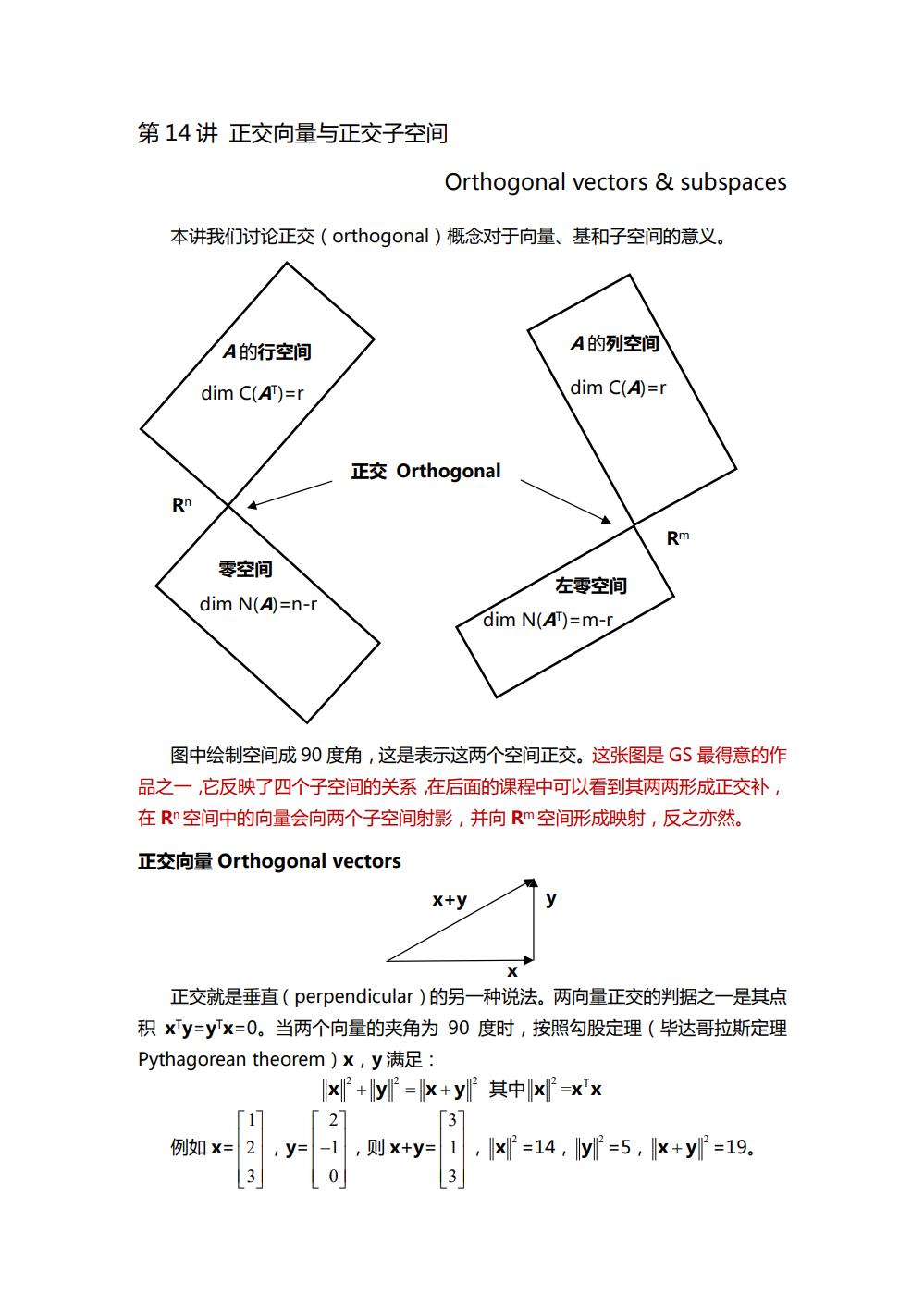
image.png
image.png
image.png
image.png

第13讲 复习一

image.png
image.png
image.png
image.png

第14讲 正交向量与正交子空间

image.png
image.png
image.png

第15讲 子空间投影

image.png
image.png
image.png

第16讲 投影矩阵和最小二乘法

image.png
image.png
image.png

第17讲 正交矩阵被施密特正交化

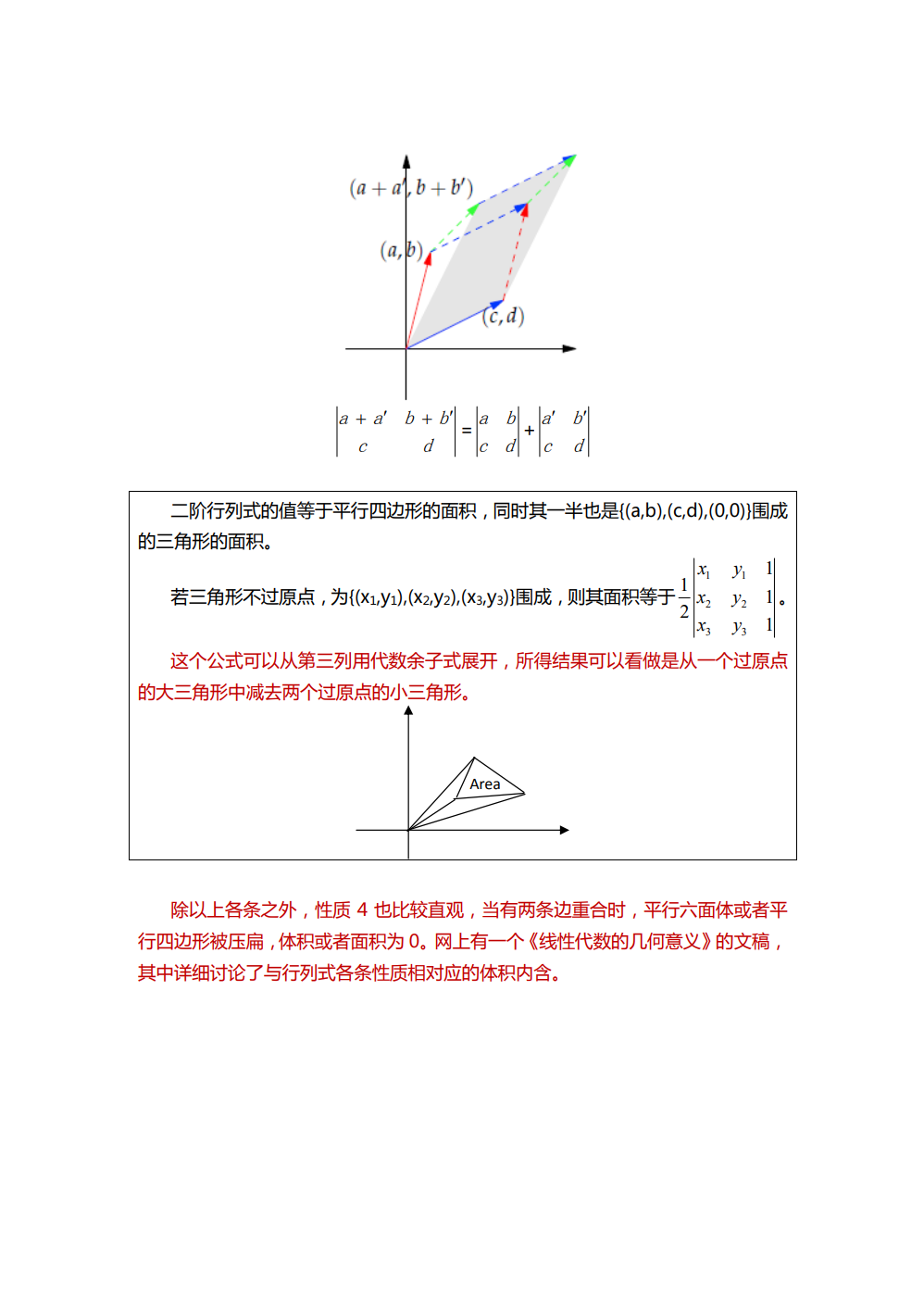
image.png
image.png
image.png

第18讲 行列式及其性质

image.png
image.png
image.png

第19讲 行列式公式和代数余子式

image.png
image.png
image.png

第20讲 克莱姆法则、逆矩阵、体积

image.png
image.png
image.png
image.png